
【题目】如图,AB为半圆O的直径,点C在半圆O上,AB=8,∠CAB=60°,P是弧![]() 上的一个点,连接AP,过点C作CD⊥AP于点D,连接BD,在点P移动过程中,BD长的最小值为_____.
上的一个点,连接AP,过点C作CD⊥AP于点D,连接BD,在点P移动过程中,BD长的最小值为_____.

【答案】2![]() ﹣2
﹣2
【解析】
以AC为直径作圆O′,连接BO′、BC.在点P移动的过程中,点D在以AC为直径的圆上运动,当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D,利用勾股定理求出BO′即可解决问题.
解:如图,以AC为直径作圆O′,连接BO′、BC,O'D,

∵CD⊥AP,
∴∠ADC=90°,
∴在点P移动的过程中,点D在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AB=8,∠CAB=60°,
∴BC=ABsin60°=![]() ,AC=ABcos60°=4,
,AC=ABcos60°=4,
∴AO'=CO'=2,
∴BO'=![]()
∵O′D+BD≥O′B,
∴当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D=![]()
故答案为![]()


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
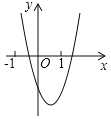
【题目】抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致是( )
在同一坐标系内的图象大致是( )
A.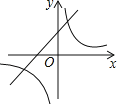 B.
B.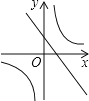
C.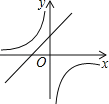 D.
D.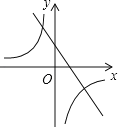
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
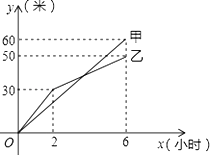
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
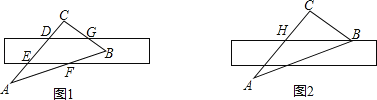
【题目】如图①,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,∠CGD=42°,将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示.
(1)∠CBH的大小为 度.
(2)点H、B的读数分别为4、13.4,求BC的长.(结果精确到0.01)
(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解 在研究函数![]() 的图象性质时,我们用“描点”的方法画出函数的图象.
的图象性质时,我们用“描点”的方法画出函数的图象.
列出表示几组![]() 与
与![]() 的对应值:
的对应值:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
描点连线:以表中各对对应值为坐标,描出各点,并用平滑的曲线顺次连接这些点,就得到函数![]() 的图象,如图1:
的图象,如图1:
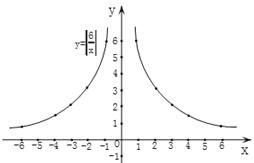
图1
可以看出,这个函数图象的两个分支分别在第一、二象限,且当![]() 时,与函数
时,与函数![]() 在第一象限的图象相同;当
在第一象限的图象相同;当![]() 时,与函数
时,与函数![]() 在第二象限的图象相同.类似地,我们把函数
在第二象限的图象相同.类似地,我们把函数![]() (
(![]() 是常数,
是常数,![]() )的图象称为“并进双曲线”.
)的图象称为“并进双曲线”.
认真观察图表,分别写出“并进双曲线”![]() 的对称性、函数的增减性性质:
的对称性、函数的增减性性质:
①图象的对称性性质: ;
②函数的增减性性质: ;
延伸探究如图2,点M,N分别在“并进双曲线”![]() 的两个分支上,
的两个分支上,![]() ,判断
,判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
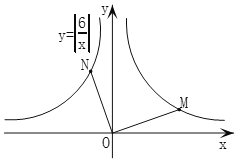
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划在某地区销售一款5G产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.该产品在第x周(x为正整数,且1≤x≤8)个销售周期的销售价格为y元,y与x之间满足如图所示的一次函数.
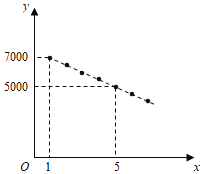
(1)求y与x之间的函数关系;
(2)产品在第x个销售周期的销售数量为p万台,p与x之间满足:![]() .已知在某个销售周期的销售收入是16000万元,求此时该产品的销售价格是多少元?
.已知在某个销售周期的销售收入是16000万元,求此时该产品的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
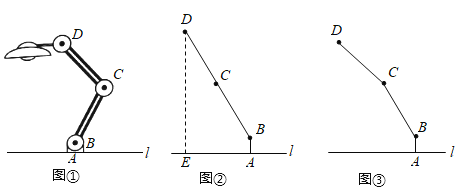
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=
与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
(1)直接写出这两个函数的关系式;
(2)求△AOC的面积;
(3)根据图象直接写出:当x为何值时,反比例函数的值小于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②![]() >0;③ac-b+1=0;④OA·OB=-
>0;③ac-b+1=0;④OA·OB=-![]() .其中结论正确的是____________
.其中结论正确的是____________
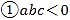
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com