
【题目】如图,在直角坐标系中,直线y=![]() x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.
x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.
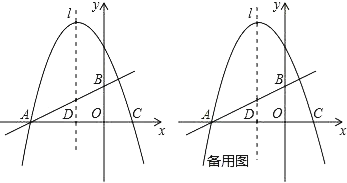
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;
(3)若点Q在第二象限内,且tan∠AQD=2,线段CQ是否存在最小值?如果存在直接写出最小值,如果不存在,请说明理由.
【答案】(1)y=﹣x2﹣2x+3;(2)点P的坐标是(﹣1,4)或(﹣2,3);(3)存在,CQ的最小值为![]() -
-![]() .
.
【解析】
(1)利用对称性和待定系数法求函数关系式;
(2)分类讨论三角形相似情况即可;
(3)由已知,满足条件的Q点在以A、D、F(﹣1,1)的圆E在第二象限的部分,连接CE交圆于Q,则CQ最小.
解:(1)∵直线y=![]() x+1与x轴交点为A,
x+1与x轴交点为A,
∴点A的坐标为(﹣3,0),
∵抛物线的对称轴为x=﹣1,
∴点C的坐标为(1,0),
∵抛物线y=﹣x2+bx+c与x轴分别交于点A、C,
∴抛物线为y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3;
(2)∵抛物线y=﹣x2﹣2x+3的对称轴为x=﹣1,
∴点D的坐标为(﹣1,0),
①当∠ADE=90°时,△ADE∽△AOB.此时点P在对称轴上,即点P为抛物线的顶点,坐标为(﹣1,4);
②当∠AED=90°时,△AED∽△AOB.
过点P作PG⊥AC于点G,则△AED∽△PGD.
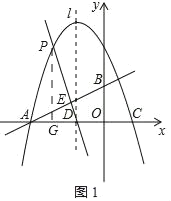
于是![]() =
=![]() =
=![]() =
=![]() ,
,
∴PG=3GD.
即:﹣t2﹣2t+3=3(﹣1﹣t),
解得 t1=﹣2,t2=3(不合题意,舍去).
当t=﹣2时,﹣22+2×2+3=3,
所以此时点P的坐标为(﹣2,3).
综上所述,点P的坐标是(﹣1,4)或(﹣2,3);
(3)存在,CQ的最小值为![]() ﹣
﹣![]() ,
,

如图,取点F(﹣1,1),过点ADF作圆,则点E(﹣2,![]() )为圆心.
)为圆心.
∵tan∠AFD=2,
∴圆弧AFD(A、D除外)上的点都是满足条件的Q点.
连CE交⊙E于点Q,则CQ为满足条件的最小值,
此时CE=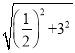 =
=![]() ,⊙E半径为
,⊙E半径为![]() ,
,
∴CQ最小值为![]() ﹣
﹣![]() .
.
故答案为:(1)y=﹣x2﹣2x+3;(2)点P的坐标是(﹣1,4)或(﹣2,3);(3)存在,CQ的最小值为![]() -
-![]() .
.


科目:初中数学 来源: 题型:
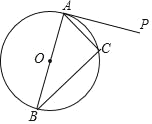
【题目】如图,△ABC为⊙O的内接三角形,其中AB为⊙O的直径,过点A作⊙O的切线PA.
(1)求证:∠PAC=∠ABC;
(2)若∠PAC=30°,AC=3,求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2.
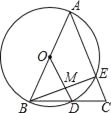
(1)求BE长;(2)求tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=
(k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=![]() ,则k的值_____.
,则k的值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
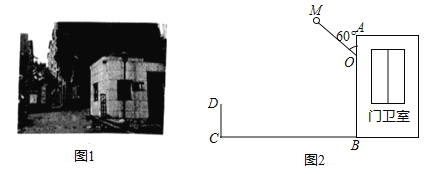
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,……,依次进行下去,若点A(![]() ,0),B(0,2),则点B2019的坐标为_____.
,0),B(0,2),则点B2019的坐标为_____.
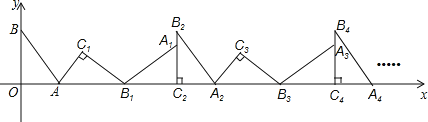
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com