
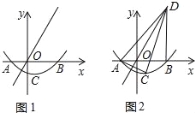
����Ŀ����ͼ1�����κ���y=a��x2��x��6����a��0����ͼ�����C��1����![]() ������x�ύ��A��B���㣨��A��x��ĸ������ϣ�����A��C�����������������y=kx��k��0����ͼ��Գƣ�
������x�ύ��A��B���㣨��A��x��ĸ������ϣ�����A��C�����������������y=kx��k��0����ͼ��Գƣ�
��1������κ����������������Ľ���ʽ��
��2����ͼ2������B��BD��x�ύ����������ͼ���ڵ�D������AC����������������ͼ���ڵ�E������AD��CD���������P�ӵ�A���߶�AD������ÿ��2����λ���ٶ���D�˶���ͬʱ����Q�ӵ�D���߶�DC������ÿ��1����λ���ٶ����C�˶���������һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�������PQ��QE��PE�����˶�ʱ��Ϊt�룬�Ƿ����ijһ�̣�ʹPE��QE�ֱ�ƽ����APQ����PQC�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1����������������ʽΪy=![]() x����2�����������
x����2�����������
��������
�����������1�����ô���ϵ�������a��ֵ�����AC�е�E���꣬��֤��OA=OC��ֱ��OE���������������������
��2�����ͼ1��ʾ���ؼ���֤����APE�ס�CEQ��������DAC=��DCA����AEP=��CQE��֤����APE�ס�CEQ�����������߶α�����ϵ�г����̣��ⷽ�����ʱ��t��ֵ��
�����������1���ѵ�C��1����![]() �����������߽���ʽy=a��x2��x��6����a=
�����������߽���ʽy=a��x2��x��6����a=![]() ��
��
�������߽���ʽΪy=![]() x2��
x2��![]() ��
��![]() ����OA=2��OC=
����OA=2��OC=![]() =2����OA=OC��
=2����OA=OC��
��A��C�е�E������Ϊ����![]() ����
����![]() ������ֱ��OE��ֱƽ��AC����A��C����ֱ��OE�Գƣ�
������ֱ��OE��ֱƽ��AC����A��C����ֱ��OE�Գƣ�
��ֱ��OE����ʽΪy=![]() x������������������������ʽΪy=
x������������������������ʽΪy=![]() x��
x��
��2��������ڣ�
���ͼ1��ʾ����Rt��ACK�У��ɹ��ɶ����ã�AC=![]() =
=![]() =2
=2![]() ����OB=3����BD=3
����OB=3����BD=3![]() ��AB=OA+OB=5����Rt��ABD�У��ɹ��ɶ����ã�AD=
��AB=OA+OB=5����Rt��ABD�У��ɹ��ɶ����ã�AD=![]() =
=![]() =2
=2![]() ��
��
����A��C����y=![]() x�Գƣ���CD=AD=2
x�Գƣ���CD=AD=2![]() ����DAC=��DCA��AE=CE=
����DAC=��DCA��AE=CE=![]() AC=
AC=![]() ��
��
����PQ��PE��QE������APE=��QPE����PQE=��CQE�����ı���APQC�У���DAC+��APQ+��PQC+��DCA=360�㣨�ı����ڽǺ͵���360�㣩����2��DAC+2��APE+2��CQE=360�㣬
���DAC+��APE+��CQE=180�㣬���ߡ�DAC+��APE+��AEP=180�㣨�������ڽǺͶ�������
���AEP=��CQE������APE����CEQ�У��ߡ�DAC=��DCA����AEP=��CQE��
���APE�ס�CEQ����![]() =
=![]() ������
������![]() ��
��![]() ��
��
�����ã�2t2��4![]() t+3=0��
t+3=0��
��ã�t=![]() ��t=
��t=![]() ��t��
��t��![]() ��������ȥ����
��������ȥ����
������ijһʱ�̣�ʹPEƽ����APQ��ͬʱQEƽ����PQC����ʱt=![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������д��һ������y��һԪһ�η��̣���ʹ���̵Ľⲻ����-1��������������һԪһ�η���Ϊ��______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=3(x-1)2+2�Ķ��������ǣ� ��
A. ��1,-2�� B. ��-1,2�� C. ��1��2�� D. ��-1��-2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����״ϸ����ֱ���ÿ�ѧ��������ʾΪ2.16��10��3�ף������ֱ���ǣ�������
A. 216000��B. 0.00216��
C. 0.000216��D. 0.0000216��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ�������ε����߳��ֱ�Ϊ2��4��������߳������ǣ� ��
A.2
B.4
C.6
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ȷ���ǣ� ��
A. 0��û�е�����û���෴��
B. �������ڱ�������ֻ����1
C. �෴�����ڱ���������������
D. ����ֵ���ڱ�������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com