
����Ŀ������������ȫ��ݡ�ƽ�����ʵ��й�������Ϊ���������·�ķ�չ�������µı�ˣ������й���ɫ������������ʱ������Ϊ���й���Ƭ���ĸ�����·Ҳ��̤���Լ��������̣������ζ�Ž��������е�·����ʱ�佫������̣���Ҳ�в����ο������ѵ�ϲ����Ȼѡ�������ͨ�г�����֪�������ص�ij�ص���ͨ�г���ʻ·����520ǧ�ף��Ǹ�����ʻ·�̵�1.3����������������⣺
(1)������ʻ��·��Ϊ_____ǧ��.
(2)��������ƽ���ٶ�(ǧ��/ʱ)����ͨ�г�ƽ���ٶ�(ǧ��/ʱ)��2.5�����ҳ�����������ʱ��ȳ�����ͨ�г�����ʱ������3Сʱ���������ƽ���ٶ�.
���𰸡�(1)400��(2)������ƽ���ٶ���300ǧ��/ʱ.
��������
��1��������ͨ�г���ʻ·����520ǧ�ף��Ǹ�����ʻ·�̵�1.3��������������ɵã�
��2������ͨ�г�ƽ���ٶ���xǧ��/ʱ���������ƽ���ٶ���2.5xǧ��/ʱ�����ݸ�������ʱ��ȳ�����ͨ�г�����ʱ������3Сʱ���г���ʽ���̣�Ȼ����⼴��.
��1��������ã�������ʻ��·��Ϊ��![]() ��ǧ�ף�
��ǧ�ף�
�ʴ�Ϊ��400��
��2������ͨ�г�ƽ���ٶ���xǧ��/ʱ���������ƽ���ٶ���2.5xǧ��/ʱ
������ã�![]()
��ã�![]()
�����飬![]() ��ԭ���̵Ľ�
��ԭ���̵Ľ�
�������ƽ���ٶ���![]() ��ǧ��/ʱ��
��ǧ��/ʱ��
�𣺸�����ƽ���ٶ���300ǧ��/ʱ.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в�����һλͬѧ�ڽⷽ��![]() ��3ʱ�Ľ����̣�
��3ʱ�Ľ����̣�
�������߶�����x����x��1+2��3����һ����
����ϲ�ͬ�����x��2���ڶ�����
�����飬x��2��ԭ���̵Ľ⣨��������
����ԭ���̵Ľ��ǣ�x��2�����IJ���
��1�����Ľ������Ǵӵ��� ������ʼ�����ģ�����ԭ������ ����
��2����д��������ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ഺ��֧���ھ���ƶ��У���������ƶ����ͥ���ͼס������������������֣���֪��������ļ۸�ȼ��������10Ԫ����480Ԫ������������Ŀ���ǡ������360Ԫ�����������Ŀ�����ͬ��
��1����ס�����������ÿ�õļ۸���Ƕ���Ԫ��
��2����ʵ�ʰ���У����Ǿ����ٴι���ס����������繲50�ã���ʱ������������ۼ۱ȵ�һ�ι���ʱ������10%������������ۼ۲��䣬����ٴι�������������ܷ��ò�����1500Ԫ����ô�������ɹ�����ٿ��������磿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AOB��
��������A'O'B'��ʹ��A'O��B'=��AOB
��1����ͼ1���Ե�OΪԲ�ģ����ⳤΪ�뾶�������ֱ�OA��OB�ڵ�C��D��
��2����ͼ2����һ������O��A�䣬�Ե�O��ΪԲ�ģ�OC��Ϊ�뾶�仡����O��A���ڵ�C�䣻
��3���Ե�C��ΪԲ�ģ�CD��Ϊ�뾶���������2���������Ļ����ڵ�D�䣻
��4������D�仭����O��B'������A'O'B'=��AOB��
����������ͼ���裬����֤����A'O'B��=��AOB��
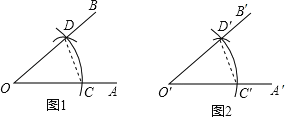
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC�У���A=90����AB=AC����DΪBC���е㣬��EDF=90����
��1�����۲췢�֣���ͼ�٣�����E��F�ֱ�ΪAB��AC�ϵĵ㣬��ͼ��ȫ��������һ���� �ԣ�
��2�������̽����������EDF�Ƶ�D��ƽ������ת������ת��E��F��ֱ���AB��CA�ӳ�����ʱ��BE=AF��������ͼ��˵�����ɣ�
��3����������⣩����EF���ѡ�EDF���Ƶ�D��ƽ������ת������ת��DF���ABC�������ڵ�ֱ�ߴ�ֱʱ����ֱ��д����BDF�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����![]() ����������
����������![]() ��
��![]() ��
��![]() ����
����![]() �����������
�����������![]() ����
����![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ٶ����߶�
����λ���ٶ����߶�![]() ���
���![]() �˶����˶�ʱ��Ϊ
�˶����˶�ʱ��Ϊ![]() �룮����
�룮����![]() ��
��![]() �ύ�������ڵ�
�ύ�������ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
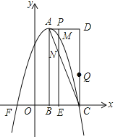
![]() ֱ��д����
ֱ��д����![]() �����꣬����������ߵĽ���ʽ��
�����꣬����������ߵĽ���ʽ��
![]() ��
��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �����������ֵΪ���٣�
�����������ֵΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABCD�ı߳�Ϊ4����E�ǶԽ���BD�ӳ�����һ�㣬AE=BD������ABE�Ƶ�A˳ʱ����ת���ȣ�0�㣼����360�㣩�õ���AB��E�䣬��B��E�Ķ�Ӧ��ֱ�ΪB�䡢E�䣮
��1����ͼ1������=30��ʱ����֤��B��C=DE��
��2������B��E��DE�䣬��B��E=DE��ʱ������ͼ2�����ֵ��
��3����ͼ3����PΪAB���е㣬��QΪ�߶�B��E��������һ�㣬��̽�����ڴ���ת�����У��߶�PQ���ȵ�ȡֵ��ΧΪ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx+b������A��0��6������ƽ����ֱ��y=-2x.
��1����ú����Ľ���ʽ������������ͼ��
��2���������ֱ�߾�����P��m��2������m��ֵ��
��3����OΪ����ԭ�㣬��ֱ��OP�Ľ���ʽ��
��4����ֱ��y=kx+b��ֱ��OP����������Χ�ɵ�ͼ�ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ÿǧ��200Ԫ�ļ۸�����ԭ��360ǧ�ˣ���������A��B���ֲ�Ʒ������1��A��Ʒ��1��B��Ʒ����ס�������ԭ�ϵ�ǧ�������±���
��Ʒ/ԭ�� | A | B |
�ף�ǧ�ˣ� | 9 | 4 |
�ң�ǧ�ˣ� | 3 | 10 |
����ԭ�ϵļ۸�Ϊÿǧ��300Ԫ��A��Ʒÿ���ۼ�3000Ԫ��B��Ʒÿ���ۼ�4200Ԫ���ֽ�����ԭ��ȫ�����꣬������A��Ʒx����B��Ʒm������˾��õ�������ΪyԪ��
��1��д��m��x�Ĺ�ϵʽ��
��2����y��x�Ĺ�ϵʽ��
��3����ʹ������ԭ�ϲ�����510ǧ�ˣ�����A�ֲ�Ʒ���ټ�ʱ����˾��������������Ϊ���٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com