
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点,∠EDF=90°.
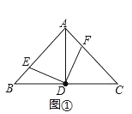
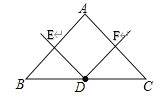
(1)(观察发现)如图①,若点E、F分别为AB、AC上的点,则图中全等三角形一共有 对;
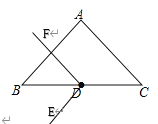
(2)(类比探究)若将∠EDF绕点D在平面内旋转,当旋转到E、F点分别在AB、CA延长线上时,BE=AF吗?请利用图②说明理由.
(3)(解决问题)连结EF,把△EDF把绕点D在平面内旋转,当旋转到DF与△ABC的腰所在的直线垂直时,请直接写出∠BDF的度数.

【答案】(1)3;(2)BE=AF;见解析;(3)45°或135°.
【解析】
(1)有3对,即△EDB≌△FDA,△EDA≌△FDC,△ADB≌△ADC.根据等腰三角形的性质可得出AD=BD、∠EBD=∠FAD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△BDE≌△ADF(ASA),其余同理可证得;
(2)根据等腰三角形的性质及等角的补角相等可得出∠EBD=∠FAD、BD=AD,根据同角的余角相等可得出∠BDE=∠ADF,由此即可证出△EDB≌△FDA(ASA),再根据全等三角形的性质即可得出BE=AF.
(3)画出符合条件的图形即可求解.
(1)有3对,即△EDB≌△FDA,△EDA≌△FDC,△ADB≌△ADC.证明如下:
∵AB=AC,点D为BC的中点,
∴∠ADB=∠ADC=90°,BD=CD,
∴△ADB≌△ADC;
∵∠EDB+∠EDA=90°,∠EDA+∠FDA=90°,
∴∠EDB=∠FDA.
在△EDB和△FDA中,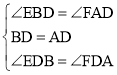 ,
,
∴△EDB≌△FDA,
同理可证△EDA≌△FDC.
(2)BE=AF,证明如下:
连接AD,如图②所示.
∵∠ABD=∠BAD=45°,
∴∠EBD=∠FAD=135°.
∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,
∴∠EDB=∠FDA.
在△EDB和△FDA中,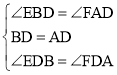 ,
,
∴△EDB≌△FDA(ASA),
∴BE=AF.
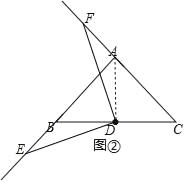
(3)45°或135°.如图所示:
∵DF⊥AC,
∴∠CDF=45°,
∴∠BDF=135°;
或者
∵DF⊥AB,
∴∠BDF=45°;
故答案是:45°或135°.


科目:初中数学 来源: 题型:
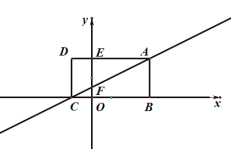
【题目】如图,矩形ABCD的边BC与x轴重合,B、C对应的横坐标是一元二次方程![]() 的两根,E是AD与y轴的交点,其纵坐标为2,过A、C作直线交y轴于F.
的两根,E是AD与y轴的交点,其纵坐标为2,过A、C作直线交y轴于F.
(1)求直线AF的解析式.
(2)M是BC上一点,其横坐标为2,在坐标轴上,你能否找到一点P,使![]() ?若能,求出点P的坐标;若不能,请说明理由.
?若能,求出点P的坐标;若不能,请说明理由.
(3)点Q是x轴上一动点,连接AQ,Q在运动过程中AQ+![]() 是否存在最小值?若存在,请求出AQ+
是否存在最小值?若存在,请求出AQ+![]() 最小值及Q的坐标;若不存在,请说明理由.
最小值及Q的坐标;若不存在,请说明理由.
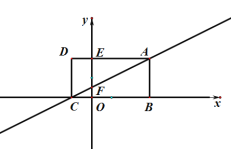
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
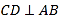
A. 4对B. 3对C. 2对D. 5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D,E是BC边上的两点,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE的度数为( )

A.10°B.20°
C.30°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路的发展树立了新的标杆,随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自已的喜好依然选择乘坐普通列车,已知从咸宁地到某地的普通列车行驶路程是520千米,是高铁行驶路程的1.3倍,请完成以下问题:
(1)高铁行驶的路程为_____千米.
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形纸片ABC中,∠C=90°,AB=12,BC=6,B′是边AC上一点.将三角形纸片折叠,使点B与点B′重合,折痕与BC、AB分别相交于E、F.设BE=x,
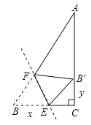
(1)若x=4,求B′C的长;
(2)当△AFB′是直角三角形时,求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交数轴于点A”,请根据图形回答下列问题:
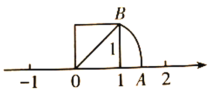
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A+∠C=180°,E、F分别在BC、CD上,且AB=BE,AD=DF,M为EF的中点,DM=3,BM=4,则五边形ABEFD的面积是_____.
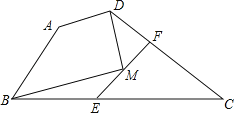
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com