
【题目】已知:三角形纸片ABC中,∠C=90°,AB=12,BC=6,B′是边AC上一点.将三角形纸片折叠,使点B与点B′重合,折痕与BC、AB分别相交于E、F.设BE=x,
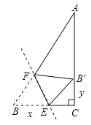
(1)若x=4,求B′C的长;
(2)当△AFB′是直角三角形时,求出x的值.
【答案】(1)![]() ;(2)x=4或2412
;(2)x=4或2412![]()
【解析】
(1)设B′C=y,根据折叠的性质得BE=B′E=4,在Rt△EB'C中利用勾股定理得y2+(6-x)2=x2,然后代入求值,解方程即可;
(2)根据锐角三角函数,得∠A=30°,由折叠的性质得到∠FB'E=∠B=60°,然后讨论:①当∠AFB'=90°时,则∠AB′F=60°,易得∠B'EC=30°,则B′C=![]() B′E,即y=
B′E,即y=![]() x,把y代入得到关于x的方程,解方程求出满足条件的x的值;②当∠AB'F=90°时,则∠EB'C=30°,即有EC=
x,把y代入得到关于x的方程,解方程求出满足条件的x的值;②当∠AB'F=90°时,则∠EB'C=30°,即有EC=![]() EB′,即6-x=
EB′,即6-x=![]() x,解方程即可.
x,解方程即可.
解:(1)设B′C=y
∵三角形纸片折叠,使点B与点B′重合,
∴BE=B′E,
∴B'E=x,CE=6-x,
在Rt△EB'C中,B'E2=CE2+B'C2,即y2+(6-x)2=x2,
当x=4时,
∴y2+(6-4)2=42
解得:![]() (负值舍去)
(负值舍去)
∴B′C′=![]() ;
;
(2)由(1)可知:y2+(6-x)2=x2,
解得:![]()
∵∠C=90°,AB=12,BC=6,
∴![]()
∴∠A=30°,
∴∠FB'E=∠B=60°,
①当∠AFB'=90°时,则∠AB′F=60°,
∴∠EB'C=60°,
∴∠B'EC=30°,
∴B′C=![]() B′E,即y=
B′E,即y=![]() x,
x,
∴![]() ,
,
解得x=24±12![]() ,
,
∵3≤x≤6,
∴x=24-12![]() ;
;
②当∠AB'F=90°时,则∠EB'C=30°,
∴EC=![]() EB′,即6-x=
EB′,即6-x=![]() x,解得x=4,
x,解得x=4,
所以x=4或2412![]() 时,△AFB’是直角三角形.
时,△AFB’是直角三角形.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】 如图,在 12×12 的正方形网格中,△TAB 的顶点分别为 T(1,1),A(2,3),B(4,2).
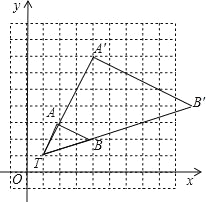
(1)以点 T(1,1)为位似中心,按比例尺(TA′:TA)3:1 的位似中心的同侧将 TAB 放大为△TA′B′,放大后点 A,B 的对应点分别为 A′,B′,画出△TA′B′,并写出点 A′,B′的坐标;
(2)在(1)中,若 C(a,b)为线段 AB 上任一点,写出变化后点 C 的对应点 C′的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
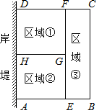
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为![]() 米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设
米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设![]() 的长度为
的长度为![]() 米,矩形区域
米,矩形区域![]() 的面积为
的面积为![]() 米
米![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点,∠EDF=90°.
(1)(观察发现)如图①,若点E、F分别为AB、AC上的点,则图中全等三角形一共有 对;
(2)(类比探究)若将∠EDF绕点D在平面内旋转,当旋转到E、F点分别在AB、CA延长线上时,BE=AF吗?请利用图②说明理由.
(3)(解决问题)连结EF,把△EDF把绕点D在平面内旋转,当旋转到DF与△ABC的腰所在的直线垂直时,请直接写出∠BDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() ,满足
,满足![]() .已知抛物线
.已知抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() .
.
![]() 求抛物线的函数关系式;
求抛物线的函数关系式;
![]() 连接
连接![]() ,点
,点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,
,![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() .一动点
.一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止.若点
后停止.若点![]() 在整个运动过程中用时最少,请直接写出最少时间和此时点
在整个运动过程中用时最少,请直接写出最少时间和此时点![]() 的坐标.
的坐标.
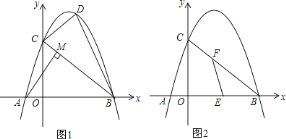
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD的边长为4,点E是对角线BD延长线上一点,AE=BD.将△ABE绕点A顺时针旋转α度(0°<α<360°)得到△AB′E′,点B、E的对应点分别为B′、E′.
(1)如图1,当α=30°时,求证:B′C=DE;
(2)连接B′E、DE′,当B′E=DE′时,请用图2求α的值;
(3)如图3,点P为AB的中点,点Q为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ长度的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com