
����Ŀ����ͼ������ABCD�ı�BC��x���غ���B��C��Ӧ�ĺ�������һԪ���η���![]() ��������E��AD��y��Ľ��㣬��������Ϊ2����A��C��ֱ�߽�y����F.
��������E��AD��y��Ľ��㣬��������Ϊ2����A��C��ֱ�߽�y����F.
��1����ֱ��AF�Ľ���ʽ��
��2��M��BC��һ�㣬�������Ϊ2�����������ϣ����ܷ��ҵ�һ��P��ʹ![]() �����ܣ������P�����ꣻ�����ܣ���˵������.
�����ܣ������P�����ꣻ�����ܣ���˵������.
��3����Q��x����һ����������AQ,Q���˶�������AQ+![]() �Ƿ������Сֵ�������ڣ������AQ+
�Ƿ������Сֵ�������ڣ������AQ+![]() ��Сֵ��Q�����ꣻ�������ڣ���˵������.
��Сֵ��Q�����ꣻ�������ڣ���˵������.
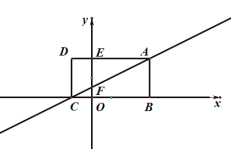
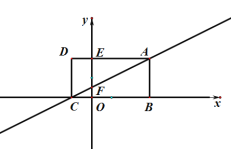
����ͼ
���𰸡���1��![]() ��2����
��2����![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
![]()
![]()
![]()
��������
��1����һԪ���η���![]() �����ɵõ���B,C�����꣬��E������Ϊ2��
�����ɵõ���B,C�����꣬��E������Ϊ2��
���ɵõ���A,C�����꣬�ô���ϵ�����������ֱ��AF�Ľ���ʽ��
��2���ֵ�P��![]() ���
���![]() �������������������.
�������������������.
![]() ����A����
����A����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ����
����![]() ��
��![]() �ڵ�M,��
�ڵ�M,��![]() ���ڵ�Q����
���ڵ�Q����![]() ��Ϊ����.
������.
��1����һԪ���η���![]() ��
��
![]()
���![]()
E��AD��y��Ľ��㣬��������Ϊ2��
![]()
��ֱ��AF�Ľ���ʽΪ![]()
�ѵ�A,C��������룬
![]()
��ã�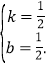
��ֱ��AF�Ľ���ʽΪ![]()
![]() ����P��
����P��![]() ����ʱ�����
����ʱ�����![]()
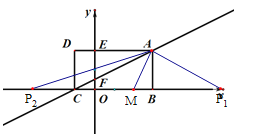
![]()
![]()
��ã�![]() ��
��![]()
��ʱ��![]() ������Ϊ
������Ϊ![]() ��
��![]()
����P��![]() ����������ʱ����
����������ʱ����![]()
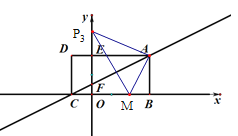
![]() =S����ABOP-
=S����ABOP-![]() -
-![]() =7.
=7.
![]()
��ã�![]()
��ʱ��![]() ������Ϊ
������Ϊ![]() .
.
����P��![]() �Ḻ������ʱ����
�Ḻ������ʱ����![]()
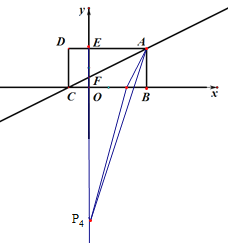
![]()
��ã�![]()
��ʱ��![]() ������Ϊ
������Ϊ![]() .
.
![]() ����A����
����A����![]() ��ĶԳƵ�
��ĶԳƵ�![]() ����
����![]() ��
��![]() �ڵ�M,��
�ڵ�M,��![]() ���ڵ�Q����
���ڵ�Q����![]() ��Ϊ����.
������.
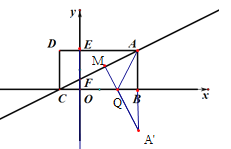
��![]() ����Ϊ
����Ϊ![]()
ֱ��![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��
ֱ��![]() ��б��
���![]()
ֱ��![]() �ķ���Ϊ��
�ķ���Ϊ�� ![]()
��![]() ʱ��
ʱ��![]()
����![]() ������Ϊ
������Ϊ![]()
��ʱ��![]()
![]()
![]()
AQ+![]() ����СֵΪ
����СֵΪ![]()


 ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ӽ��Ž����Ӽ����ݣ���Ա�����ΰ��Ҷ�A�����������ݶ�������B����������(����һ��)��·����������![]() ��һ���֣���ͼ
��һ���֣���ͼ

��1������Ա�������������߶ȣ�
��2����֪���ݸ�BC��3.4�ף���һ�α����У����ݵ�������A��ˮƽ������4�ף�����α����Ƿ�ɹ�����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB��AC��BC��12���ף���DΪAB��һ����BD��8���ף���P���߶�BC����2����/����ٶ���B����C���˶������˶�ʱ��Ϊt��ͬʱ����Q���߶�CA����C����A���˶�.

��1���ú�t��ʽ�ӱ�ʾPC�ij�Ϊ_______________;
��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2ʱ��������BPD��������CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��3������Q���˶��ٶ����P���˶��ٶȲ���ȣ��������Q���˶��ٶ��Ƕ���ʱ���ܹ�ʹ������BPD��������CQPȫ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����˵����ƳǼ��г����Ѿ���ͨ����������������⣺��ͼ�������ӻ�ʯA���ͳ����������վB�����ڿ����ڻ�ʯA������ƳǼ��г������人��ɽվC���ٴ���ɽվC�����ڹ����������������վB.��AB��80 km��BC��20 km����ABC��120��.�������С������������⣺
(1)��A��C֮��ľ��룮(�ο�����![]() ��4.6)
��4.6)
(2)���ͳ���ƽ���ٶ���60 km/h�����ڵĹ���������ƽ���ٶ�Ϊ40 km/h������ƳǼ��г�����ƽ���ٶ�Ϊ180 km/h��Ϊ�������ʱ���ڵ����������վ��С��Ӧѡ�����ֳ˳���������˵�����ɣ�(���ƺ�ʱ��)
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
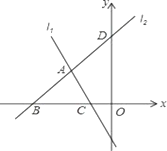
����Ŀ����ͼ��ֱ��l1��l2���ڵ�A��ֱ��l2��x�ᡢy��ֱ��ڵ�B����3��0����D��0��3����ֱ��l1����Ӧ�ĺ�����ϵʽΪy=��2x��2��
��1�����C�����꼰ֱ��l2����Ӧ�ĺ�����ϵʽ��
��2������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в�����һλͬѧ�ڽⷽ��![]() ��3ʱ�Ľ����̣�
��3ʱ�Ľ����̣�
�������߶�����x����x��1+2��3����һ����
����ϲ�ͬ�����x��2���ڶ�����
�����飬x��2��ԭ���̵Ľ⣨��������
����ԭ���̵Ľ��ǣ�x��2�����IJ���
��1�����Ľ������Ǵӵ��� ������ʼ�����ģ�����ԭ������ ����
��2����д��������ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ,�� 12��12 ��������������,��TAB �Ķ���ֱ�Ϊ T(1,1),A(2,3),B(4,2).
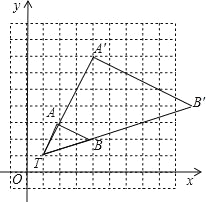
(1)�Ե� T(1,1)Ϊλ������,��������(TA��:TA)3:1 ��λ�����ĵ�ͬ�ཫ TAB �Ŵ�Ϊ��TA��B��,�Ŵ��� A,B �Ķ�Ӧ��ֱ�Ϊ A��,B��,������TA��B��,��д���� A��,B������ꣻ
(2)��(1)��,�� C(a,b)Ϊ�߶� AB ����һ��,д���仯��� C �Ķ�Ӧ�� C������ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɱ߳�Ϊ1��С�����ι��ɵ�����ÿ��С�����εĶ��������㣬![]() �Ķ����ڸ���ϣ���
�Ķ����ڸ���ϣ���![]() ����
����![]() Ϊԭ�㽨��ƽ��ֱ������ϵ��ƽ����
Ϊԭ�㽨��ƽ��ֱ������ϵ��ƽ����![]() ���ֱ��
���ֱ��![]() ����
����![]() ���밴Ҫ������������.
���밴Ҫ������������.
��1������![]() ����ֱ��
����ֱ��![]() �ĶԳ�
�ĶԳ�![]() ����ֱ��д����
����ֱ��д����![]() �ĶԳƵ�
�ĶԳƵ�![]() �����ꣻ
�����ꣻ
��2�����![]() ��
��![]() �ľ��룻
�ľ��룻
��3����![]() ���Ҳ�ĸ������һ��
���Ҳ�ĸ������һ��![]() ��ʹ
��ʹ![]() ����ֱ��д��
����ֱ��д��![]() �������.
�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
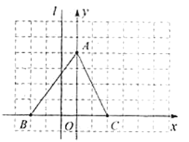
����Ŀ����֪���ڡ�ABC�У���A=90����AB=AC����DΪBC���е㣬��EDF=90����
��1�����۲췢�֣���ͼ�٣�����E��F�ֱ�ΪAB��AC�ϵĵ㣬��ͼ��ȫ��������һ���� �ԣ�
��2�������̽����������EDF�Ƶ�D��ƽ������ת������ת��E��F��ֱ���AB��CA�ӳ�����ʱ��BE=AF��������ͼ��˵�����ɣ�
��3����������⣩����EF���ѡ�EDF���Ƶ�D��ƽ������ת������ת��DF���ABC�������ڵ�ֱ�ߴ�ֱʱ����ֱ��д����BDF�Ķ���.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com