
����Ŀ����ͼ����֪�ڡ�ABC�У�AB��AC��BC��12���ף���DΪAB��һ����BD��8���ף���P���߶�BC����2����/����ٶ���B����C���˶������˶�ʱ��Ϊt��ͬʱ����Q���߶�CA����C����A���˶�.

��1���ú�t��ʽ�ӱ�ʾPC�ij�Ϊ_______________;
��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2ʱ��������BPD��������CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��3������Q���˶��ٶ����P���˶��ٶȲ���ȣ��������Q���˶��ٶ��Ƕ���ʱ���ܹ�ʹ������BPD��������CQPȫ��?
���𰸡�(1)PC=12-2t��(2)��BPD����CQP���ɼ���⣻(3) ![]() cm/s
cm/s
��������
(1)����BC=12cm����P���߶�BC����2����/����ٶ���B����C���˶������Ե�t��ʱ���˶�2t�����PC=12-2t.��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2sʱ����CQ=4cm��BP=4cm����ΪBC=12cm������PC=8cm,����ΪBD=8cm��AB=AC�����ԡ�B=��C,��������BPD�զ�CQP.(3) ��֪��B=��C��BP��CQ�����ݦ�BPD�զ�CQP�ó� BP=PC���������ʱ��t�������v����.
(1)�������PC=12-2t
��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2sʱ����CQ=4cm��BP=4cm���� BC=12cm����PC=8cm,�֡�BD=8cm��AB=AC�����B=��C���ڦ�BPD�ͦ�CQP�У�CQ=BP, ��B=��C,PC=BD���তBPD�զ�CQP��SAS��.
(3)����Q���˶��ٶ����P���˶��ٶȲ���ȣ���Vp��VQ,��BP��CQ,�֡ߡ�BPD�ա�CPQ,��B=��C,��BP=PC=6cm,CQ=BD=8cm,���P����Q�˶���ʱ�� t= ![]() =3s ,
=3s ,
��VQ =![]() =
=![]() =
=![]() cm/s����Q���ٶ�Ϊ
cm/s����Q���ٶ�Ϊ![]() cm/s.
cm/s.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������������ABCD����࣬����ADE����DCF������AF��BE.����̽������ͼ������ADE����DCF��Ϊ�ȱ������Σ����ж��߶�AF��BE��������ϵ��λ�ù�ϵ����˵������.
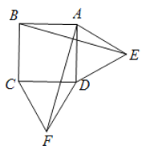
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ֽƬABCD�ع���B��ֱ���۵���ʹ��A����BC���ϵĵ�F�����ۺ�ΪBE(��ͼ1)�����ع���E��ֱ���۵���ʹ��D����BE�ϵĵ�D�������ۺ�ΪEG(��ͼ2)����չƽֽƬ(��ͼ3)����ͼ3�С����Ĵ�СΪ()
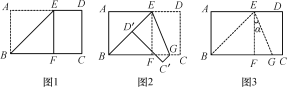
A.30��B.25.5��C.20��D.22.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ABC�С�BAC=150�㣬AB��AC�Ĵ�ֱƽ���߷ֱ�BC��E��F.���EAF�Ķ���Ϊ______��
ABC�С�BAC=150�㣬AB��AC�Ĵ�ֱƽ���߷ֱ�BC��E��F.���EAF�Ķ���Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
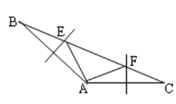
����Ŀ����ͼ������ABC����DEF�У�AB��DE����A��F��C��D��ͬһֱ���ϣ�AF��CD����AFE����BCD��
��˵����
��1����ABC�ա�DEF��
��2��BF��EC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��(��![]() )2 017��161 008��
)2 017��161 008��
��2��(8a6b3)2��(��2a2b)��
��3����ʽ�ֽ⣺a2b-b3
��4����ʽ�ֽ⣺��3x3+6x2y��3xy2
��5���ⷽ�̣�![]()
��6���ⷽ�̣�![]() =0��
=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���ABC��90����AB��4��BC��3��CD��12��AD��13�����ı���ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�BC��x���غ���B��C��Ӧ�ĺ�������һԪ���η���![]() ��������E��AD��y��Ľ��㣬��������Ϊ2����A��C��ֱ�߽�y����F.
��������E��AD��y��Ľ��㣬��������Ϊ2����A��C��ֱ�߽�y����F.
��1����ֱ��AF�Ľ���ʽ��
��2��M��BC��һ�㣬�������Ϊ2�����������ϣ����ܷ��ҵ�һ��P��ʹ![]() �����ܣ������P�����ꣻ�����ܣ���˵������.
�����ܣ������P�����ꣻ�����ܣ���˵������.
��3����Q��x����һ����������AQ,Q���˶�������AQ+![]() �Ƿ������Сֵ�������ڣ������AQ+
�Ƿ������Сֵ�������ڣ������AQ+![]() ��Сֵ��Q�����ꣻ�������ڣ���˵������.
��Сֵ��Q�����ꣻ�������ڣ���˵������.
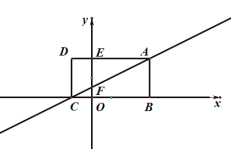
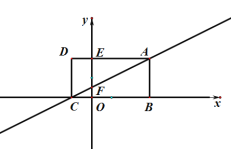
����ͼ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,CD��AB,BE��AC,����ֱ�Ϊ��D,��E,BE��CD�ཻ�ڵ�O.��1=��2,��ͼ��ȫ�������ι���( )
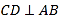
A. 4��B. 3��C. 2��D. 5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com