【题目】将长方形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE(如图1)；再沿过点E的直线折叠，使点D落在BE上的点D′处，折痕为EG(如图2)；再展平纸片(如图3)，则图3中∠α的大小为()
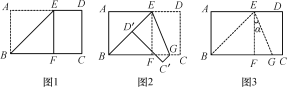
A.30°B.25.5°C.20°D.22.5°
浙江名校名师金卷系列答案科目：初中数学 来源： 题型：
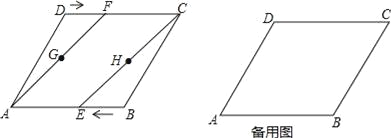
【题目】如图，在菱形ABCD中，AB=4cm，∠BAD=60°．动点E、F分别从点B、D同时出发，以1cm/s的速度向点A、C运动，连接AF、CE，取AF、CE的中点G、H，连接GE、FH．设运动的时间为ts（0＜t＜4）．
（1）求证：AF∥CE；
（2）当t为何值时，四边形EHFG为菱形；
（3）试探究：是否存在某个时刻t，使四边形EHFG为矩形，若存在，求出t的值，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体(看成一点)的路线是抛物线
的一部分，如图
（1）求演员弹跳离地面的最大高度；
（2）已知人梯高BC＝3.4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知等腰
中，
，点
从点
出发在线段
移动，以
为腰作等腰
，
，连接
.
（1）如图，求证：
≌
；
（2）求证：
；
（3）若
，试问：
的面积有没有最大值，如没有请说明理由，如有请求出最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果一个分式能化成一个整式与一个分子为常数的分式的和的形式，则称这个分式为“快乐分式”.如：
，则 
是“快乐分式”．
(1)下列式子中，属于“快乐分式”的是 （填序号）；
①
，② 
，③
，④ 
.
（2）将“快乐分式”
化成一个整式与一个分子为常数的分式的和的形式为： = .
（3）应用：先化简
，并求x取什么整数时，该式的值为整数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ACD和△BCE中， AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P，则∠BPD的度数为（ ）
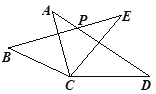
A.110°B.125°C.130°D.155°
查看答案和解析>>
科目：初中数学 来源： 题型：
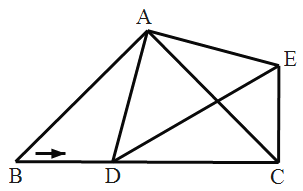
【题目】如图，已知在△ABC中，AB＝AC，BC＝12厘米，点D为AB上一点且BD＝8厘米，点P在线段BC上以2厘米/秒的速度由B点向C点运动，设运动时间为t，同时，点Q在线段CA上由C点向A点运动.
（1）用含t的式子表示PC的长为_______________;
（2）若点Q的运动速度与点p的运动速度相等，当t＝2时，三角形BPD与三角形CQP是否全等，请说明理由；
（3）若点Q的运动速度与点P的运动速度不相等，请求出点Q的运动速度是多少时，能够使三角形BPD与三角形CQP全等?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图,在 12×12 的正方形网格中,△TAB 的顶点分别为 T(1,1),A(2,3),B(4,2).
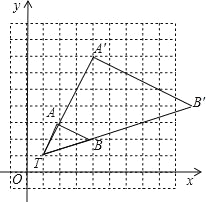
(1)以点 T(1,1)为位似中心,按比例尺(TA′:TA)3:1 的位似中心的同侧将 TAB 放大为△TA′B′,放大后点 A,B 的对应点分别为 A′,B′,画出△TA′B′,并写出点 A′,B′的坐标；
(2)在(1)中,若 C(a,b)为线段 AB 上任一点,写出变化后点 C 的对应点 C′的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
