
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
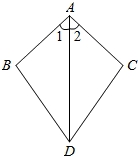
A.AB=AC B.BD=CD C.∠ B=∠C D.∠BDA=∠CDA
B=∠C D.∠BDA=∠CDA
B【考点】全等三角形的判定.
【专题】压轴题.
【分析】利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.
【解答】解:A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意;
B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意;
C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);故C不符合题意;
D、∵∠1=∠2,AD为公共边,若∠BDA=∠CDA,则△ABD≌△ACD(ASA);故D不符合题意.
故选:B.
【点评】此题主要考查学生对全等三角形判定定理的理解和掌握,此题难度不大,属于基础题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
在江阴市开展的创建文明城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园 ,花园的一边靠墙,另三边用总长为40m的栅栏围
,花园的一边靠墙,另三边用总长为40m的栅栏围 成(如
成(如
图所示).若设花园的
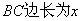 (m),花园的面积为
(m),花园的面积为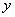
 (m
(m ).
).
(1)求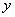 与
与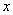 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量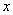 的取值范围;
的取值范围;
(2)满足条件的花园面积能达到200 m 吗?
吗?
若能,求出此时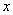 的值;若不能,说明理由;
的值;若不能,说明理由;
(3)当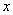 取何值时,花园的面积最大?最大面积为多少?
取何值时,花园的面积最大?最大面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(2k+1)x+4(k﹣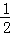 )=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
)=0,若等腰三角形ABC的一边长a=4,另一边长b、c恰好是这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com