
【题目】如图,在△ABD和△ACD中,已知AB=AC,∠B=∠C,求证:AD是∠BAC的平分线. 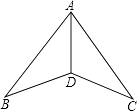
【答案】证明:连接BC,
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABD=∠ACD,
∴∠DBC=∠DCB.
∴BD=CD.
在△ADB和△ADC中,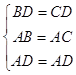 ,
,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD,
即AD是∠BAC的平分线.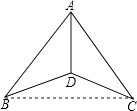
【解析】连接BC,由AB=AC得到∠ABC=∠ACB,已知∠ABD=∠ACD,从而得出∠DBC=∠DCB,即BD=CD,又因为AB=AC,AD=AD,利用SSS判定△ABD≌△ACD,全等三角形的对应角相等即∠BAD=∠CAD,所以AD是∠BAC的平分线.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.


科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一长方形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,求△CEF的面积. 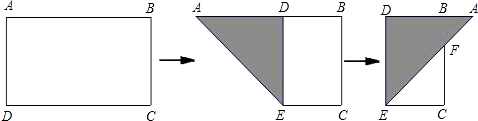
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有颜色分别为红、黄、蓝的球各一个,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,恰好是红球的概率为 ;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,通过树状图或表格列出所有等可能性结果,并求两次都是摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列命题中,正确的是( )
A. 有一组对边平行的四边形是平行四边形 B. 有一组邻边相等的平行四边形是菱形
C. 有一个角是直角的四边形是矩形 D. 对角线互相垂直平分的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com