
【题目】如图,有一长方形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,求△CEF的面积. 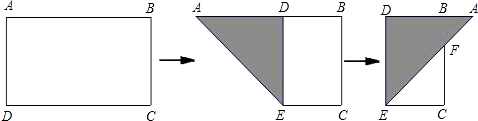
【答案】解:如下图所示: 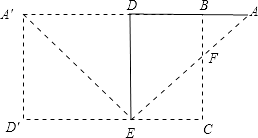
由对称的性质可知:A′D′=A′D=AD=6,BD=10﹣6=4,
∴AB=6﹣4=2.
易证Rt△ADE∽Rt△ABF,
∴ ![]()
∴BF= ![]() =
= ![]() =2
=2
∴S△CEF= ![]() ABBF=
ABBF= ![]() ×2×2=2,
×2×2=2,
即:△CEF的面积为2.
【解析】由翻折变换(轴对称)的性质可知:AD=6,BD=10﹣6=4,AB=6﹣4=2,再证明Rt△ADE∽Rt△ABF,从而得出BF的长,由此可计算出△CEF的面积.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
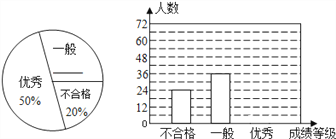
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有达标率为 ;
(3)若该校学生有学生3000人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB,下列确定P点的方法正确的是( ) 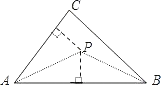
A.P是∠A与∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为A
D.AB两边上的高的交点
E.P为A
F.AB两边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,1),B(2,0),C(4,3)
(1)画出△ABC,请求△ABC的面积;
(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,求P点的坐标. 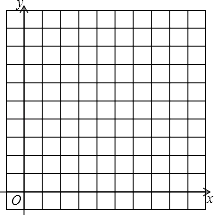
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请用“<”或“>”连接下面的式子.
(1)4______-6 (2)-8______-3
(3)-4.5_______-4 (4)7+(-3)_________4+(-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】团体购买公园门票票价如下:
购票人数(人) | 1~50 | 51~100 | 100以上 |
每人门票(元) | 13 | 11 | 9 |
今有甲、乙两个旅行团,已知甲团人数少于50人,乙团人数不超过100人.若分别购票,两团共计应付门票费1392元,若合在一起作为一个团体购票,总计应付门票费1080元.
(1)请你判断乙团的人数是否也少于50人;
(2)求甲、乙两旅行团各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数为( )
①过一点有无数条直线与已知直线平行; ②如果a∥b,a∥c,那么b∥c;
③如果两线段不相交,那么它们就平行; ④如果两直线不相交,那么它们就平行.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com