
【题目】已知点A(0,1),B(2,0),C(4,3)
(1)画出△ABC,请求△ABC的面积;
(2)设点P在坐标轴上,且△ABP与△ABC的面积相等,求P点的坐标. 
【答案】
(1)解:如图所示:
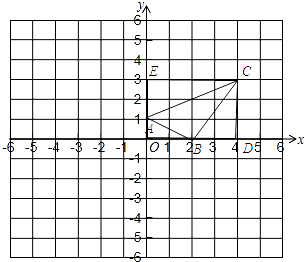
(2)解:过点C向x、y轴作垂线,垂足为D、E.
∴四边形DOEC的面积=3×4=12,△BCD的面积= ![]() =3,△ACE的面积=
=3,△ACE的面积= ![]() =4,△AOB的面积=
=4,△AOB的面积= ![]() =1.
=1.
∴△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
=12﹣3﹣4﹣1=4.
当点p在x轴上时,△ABP的面积= ![]() =4,即:
=4,即: ![]() ,解得:BP=8,
,解得:BP=8,
所点P的坐标为(10,0)或(﹣6,0);
当点P在y轴上时,△ABP的面积= ![]() =4,即
=4,即 ![]() ,解得:AP=4.
,解得:AP=4.
所以点P的坐标为(0,5)或(0,﹣3).
所以点P的坐标为(0,5)或(0,﹣3)或(10,0)或(﹣6,0).
【解析】(1)确定出点A、B、C的位置,连接AC、CB、AB即可;(2)过点C向x、y轴作垂线,垂足为D、E,△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积;(3)当点p在x轴上时,由△ABP的面积=4,求得:BP=8,故此点P的坐标为(10,0)或(﹣6,0);当点P在y轴上时,△ABP的面积=4,解得:AP=4.所以点P的坐标为(0,5)或(0,﹣3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】商场销售甲、乙两种商品,它们的进价和售价如表,
进价(元) | 售价(元) | |
甲 | 15 | 20 |
乙 | 35 | 43 |
(1)若该商场购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)该商场为使销售甲、乙两种商品共100件的总利润(利润=售价﹣进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市区有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,现准备进行绿化,中间的有一边长为(a+b)米的正方形区域将修建一座雕像,则绿化的面积是多少平方米?并求出当a=5,b=3时的绿化面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校成立“情暖校园”爱心基金会,去年上半年发给每个经济困难的学生600元,今年上半年发给了800元,设每半年发给的资金金额的平均增长率为x,则下面列出的方程中正确的是( )
A.800(1﹣x)2=600
B.600(1﹣x)2=800
C.800(1+x)2=600
D.600(1+x)2=800
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一长方形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,求△CEF的面积. 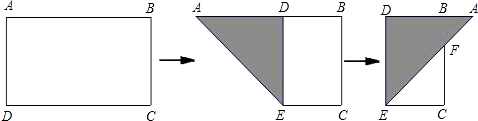
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列命题中,正确的是( )
A. 有一组对边平行的四边形是平行四边形 B. 有一组邻边相等的平行四边形是菱形
C. 有一个角是直角的四边形是矩形 D. 对角线互相垂直平分的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形四边条边都相等,四个角都是90°.如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG. 
(1)如图1,当点E在线段BC上(不与点B、C重合)时: 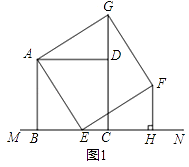
①判断△ADG与△ABE是否全等,并说明理由;
②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;
(2)如图2,当点E在射线CN上(不与点C重合)时: 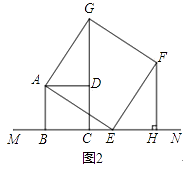
①判断△ADG与△ABE是否全等,不需说明理由;
②过点F作FH⊥MN,垂足为点H,已知GD=4,求△CFH的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com