
����Ŀ���������ı����߶���ȣ��ĸ��Ƕ���90�㣮��ͼ����֪������ABCD��ֱ��MN���Ϸ���BC��ֱ��MN�ϣ���E��ֱ��MN��һ�㣬��AEΪ����ֱ��MN���Ϸ���������AEFG�� 
��1����ͼ1������E���߶�BC�ϣ������B��C�غϣ�ʱ�� 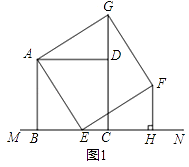
���жϡ�ADG���ABE�Ƿ�ȫ�ȣ���˵�����ɣ�
�ڹ���F��FH��MN������Ϊ��H���۲첢�²��߶�BE���߶�CH��������ϵ����˵�����ɣ�
��2����ͼ2������E������CN�ϣ������C�غϣ�ʱ�� 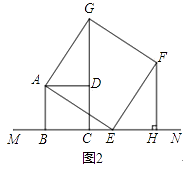
���жϡ�ADG���ABE�Ƿ�ȫ�ȣ�����˵�����ɣ�
�ڹ���F��FH��MN������Ϊ��H����֪GD=4�����CFH�������
���𰸡�
��1���⣺�١�BAE�ա�DAG���������£�
���ı���ABCD���ı���AEFG�������Σ�
��AB=AD��AE=AG����BAD=��EAG=90�㣬
���BAE+��EAD=��DAG+��EAD��
���BAE=��DAG��
���BAE�ա�DAG��
��CH=BE���������£�
����֪�ɵá�EAG=��BAD=��AEF=90�㣬
�ɢٵá�FEH=��BAE=��DAG��
�֡�G������CD�ϣ�
��GDA=��EHF=��EBA=90�㣬AG=AE=EF��
���BAE=��DAG=��EFH��
���EFH�ա�GAD����EFH�ա�ABE��
��EH=AD=BC��
��CH=BE��
��2���⣺�١�BAE�ա�DAG���������£�
���ı���ABCD���ı���AEFG�������Σ�
��AB=AD��AE=AG����ADG=��ABE=90�㣬
����Rt��BAE��Rt��DAG��
���BAE�ա�DAG����HL��
���ɣ�1��ͬ���ɵã���EFH�ա�AGD����EFH�ա�AEB��
��GD=FH=CH=4��
���CFH������� ![]() FHCH=
FHCH= ![]() ��4��4=8
��4��4=8
����������1�������������ε����ʼ�SAS���������ADG�ա�ABE��������ȫ�������ε����ʼ��ɽ�𣻢����������ε����ʼ�SAS���������ADG�ա�ABE��������ȫ�������ε����ʼ��ɽ�𣻣�2��������HL����֤����BAE�ա�DAG���ɣ������á�EFH�ա�GAD����EFH�ա�ABE�����ɵó�GD=FH=CH=4�������á�CFH�������ʽ�����


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��0��1����B��2��0����C��4��3��
��1��������ABC�������ABC�������
��2�����P���������ϣ��ҡ�ABP���ABC�������ȣ���P������꣮ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ�ĸ���Ϊ( )
�ٹ�һ����������ֱ������ֱ֪��ƽ�У� �����a��b��a��c����ôb��c��
��������߶β��ཻ����ô���Ǿ�ƽ�У� �������ֱ�߲��ཻ����ô���Ǿ�ƽ�У�
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��9=0�ĸ��ǣ� ��
A.x=3
B.x=��3
C.x1=3��x2=��3
D.x1=9��x2=��9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���OBCD�е����������ڡ�O�ϣ���A�ǡ�O�ϵ�һ������(�����B��C��D�غ�)�����ı���OBCD��ƽ���ı���ʱ����ô![]() ��������ϵ��________________.
��������ϵ��________________.
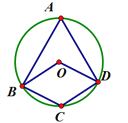
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ڷ���ֽ��
��1�����ڷ���ֽ�Ͻ���ƽ��ֱ������ϵ��ʹA��2��3����C��6��2���������B�����ꣻ
��2����ԭ��OΪλ�����ģ����Ʊ�Ϊ2���ڵ�һ�����ڽ���ABC�Ŵ����Ŵ���ͼ����A��B��C����
��3��������A��B��C�������S��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ε����߳�Ϊ2��9,�����߳��Ƿ���x2��14x+48=0��һ�������������ε��ܳ�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �����ڿ����˷��̣�1���е�a���õ�������Ľ�Ϊ
�����ڿ����˷��̣�1���е�a���õ�������Ľ�Ϊ![]() �� �����ڿ����˷��̣�2���е�b���õ�������Ľ�Ϊ
�� �����ڿ����˷��̣�2���е�b���õ�������Ľ�Ϊ![]() �� ������ȷ�ļ��㣬��x+6y��ֵ��
�� ������ȷ�ļ��㣬��x+6y��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com