
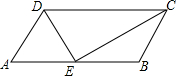
 已知,如图,在平行四边形ABCD中,AB=2AD,E为AB的中点,连接DE,EC,求证:DE⊥EC.
已知,如图,在平行四边形ABCD中,AB=2AD,E为AB的中点,连接DE,EC,求证:DE⊥EC. 分析 利用平行四边形的性质和已知条件易证DE,CE分别是∠ADC和∠DCB的角平分线,由角平分线的性质可得∠EDC+∠ECD=90°,则∠DEC=90°,即DE⊥EC.
解答 证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠ADC+∠BCD=180°,
∴∠AED=∠CDE,
∵E为AB的中点,
∴AE=BE,
∵AB=2AD,
∴AD=AE,
∴∠ADE=∠AED,
∴∠ADE=∠CDE,
同理可证:∠DCE=∠BCE,
∴∠EDC+∠ECD=$\frac{1}{2}$×180°=90°,
∴∠DEC=90°,
即DE⊥EC.
点评 本题考查了平行四边形的性质、等腰三角形的判定和性质以及角平分线的性质和三角形内角和定理的运用,解题的关键利用平行四边形的性质得到DE,CE分别是∠ADC和∠DCB的角平分线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等 | |
| B. | 互为相反数 | |
| C. | 当n为奇数时它们互为相反数,当n为偶数时相等 | |
| D. | 当n为奇数时相等,当n为偶数时互为相反数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
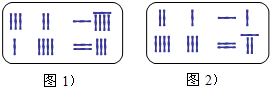 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )
《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是$\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$,类似地,图2所示的算筹图我们可以表述为( )| A. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=27}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=11}\\{4x+3y=22}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+2y=19}\\{x+4y=23}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{4x+3y=27}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
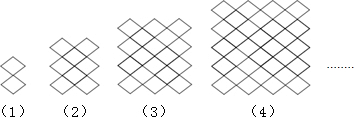
| A. | 32 | B. | 36 | C. | 50 | D. | 72 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com