
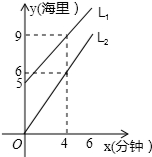
 L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象如图.
L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象如图.分析 (1)先设出l1、l2的函数表达式,再用待定系数法进行求解,即可得出答案;
(2)公安快艇追上走私船时令y1=y2,再进行求解即可.
解答 解:(1)设l1的函数表达式是y1=k1x+b,
l2的函数表达式是y2=k2x,
由图象可知,l1过点(0,5)、(4,9),
$\left\{\begin{array}{l}{9={4k}_{1}+b}\\{b=5}\end{array}\right.$,
解得k1=1,
l1的函数表达式是y1=x+5,
由图象可知,l2过点(4,6),
6=4k2,
解得:k2=$\frac{3}{2}$,
l2的函数表达式是y2=$\frac{3}{2}$x.
(2)根据题意得:
x+5=$\frac{3}{2}$x,
解得x=10.
答:公安快艇10分钟能追上走私船.
点评 本题考查了一次函数的应用,同时也考查了识别函数图象的能力,观察图象提供的信息,再分析求解是本题的关键.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
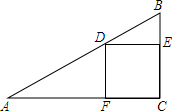 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.
如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +8 | -9 | +10 | +4 | -6 | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com