
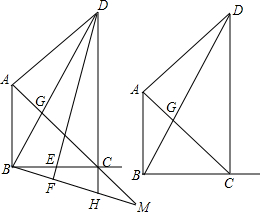
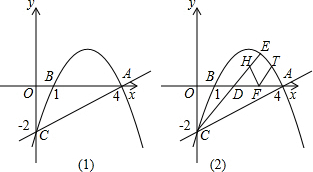
���� ��1������������������CD=6������BF��DE��FΪ�߶�BH�е���������ɵ������������ߺ�һ�����ʵõ���BHDΪ���������Σ��Ӷ����BD=HD=3$\sqrt{5}$������CH=3$\sqrt{5}$-6��
��2����BE=x��CM=y��Ҫ��y����x�ĺ�������ʽ��������AB��CH���õ��ɱ����߶�$\frac{CH}{AB}$=$\frac{CM}{AM}$���õ�$\frac{CH}{3}$=$\frac{y}{y+3\sqrt{2}}$���ٸ��ݡ�BCH�ס�DCE���õ�$\frac{CH}{CE}$=$\frac{BC}{DC}$=$\frac{3}{6}$��������ú�x��ʽ�ӱ�ʾCH=$\frac{3-x}{2}$������$\frac{CH}{3}$=$\frac{y}{y+3\sqrt{2}}$ �У���������ɵ�y=$\frac{9\sqrt{2}-3\sqrt{2}x}{3+x}$�����ݵ�E���߶�BC�ϣ���ɵõ�0��x��3��
��3��������ͼ2����GF��BCʱ����ʱGF��AB��CD������ƽ���ߵȷ��߶ζ����õ�$\frac{BG}{GD}$=$\frac{BF}{FH}$=$\frac{1}{2}$������������֤��BCH�ס�DCE�����������Ʊȵ�BF=$\frac{1}{3}$BH=$\frac{1}{6}$DE���ٸ��ݡ�BFE�ס�DCE�����Ʊ�$\frac{BF}{DC}$=$\frac{BE}{DE}$�õ�$\frac{\frac{1}{6}DE}{6}$=$\frac{x}{DE}$���ⷽ�̼��ɵ�x=21-6$\sqrt{11}$ ������x=21+6$\sqrt{11}$��3����ȥ���ڵ�E������BC��ʱ��ͼ3����GF��BE����GF��CD����ΪK���ȸ��ݢ������������GK=2��DK=4����KF=a����ɵ�$\frac{a}{3}$=$\frac{KH}{HC}$=$\frac{KH}{2-KH}$���ֱ��ú�a��ʽ�ӱ�ʾKH=$\frac{2a}{3+a}$��HC=$\frac{6}{3+a}$��������tan��KDF=tan��CBH��Ϊ������ϵ�з���$\frac{a}{4}$=$\frac{\frac{6}{3+a}}{3}$�ɽ��a=$\frac{-3+\sqrt{41}}{2}$��a=$\frac{-3-\sqrt{41}}{2}$��0����ȥ�������CE=$\frac{3}{2}$a=$\frac{-9+3\sqrt{41}}{4}$�Ӷ����BE=CE+3=$\frac{3+3\sqrt{41}}{4}$�����ۺϢ٢ڿ�֪x��ֵΪ21-6$\sqrt{11}$ ��$\frac{3+3\sqrt{41}}{4}$��
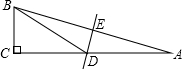
��� �⣺��1������ֱ������ABCD�У�AB��CD����ABC=90��
���DCB=90��
��AB=BC=3��tan��BDC=$\frac{1}{2}$
��CD=6
��BF��DE
�൱FΪ�߶�BH�е�ʱ����BHDΪ���������Σ�
��BD=HD=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$
CH=DH-DC=3$\sqrt{5}$-6
��2����AB��CH��
��$\frac{CH}{AB}$=$\frac{CM}{AM}$
�֡�AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$��
��$\frac{CH}{3}$=$\frac{y}{y+3\sqrt{2}}$
�ڡ�BCH���DCE�У�
��BCH=��DCE=90�㣬��HBC=��EDC=90��-��DHB��
���BCH�ס�DCE��
��$\frac{CH}{CE}$=$\frac{BC}{DC}$=$\frac{3}{6}$����CH=$\frac{3-x}{2}$��
��$\frac{\frac{3-x}{2}}{3}$=$\frac{y}{y+3\sqrt{2}}$�����������ã�y=$\frac{9\sqrt{2}-3\sqrt{2}x}{3+x}$��0��x��3����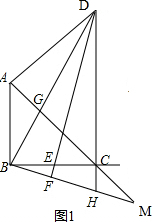
��3���٣�ͼ2��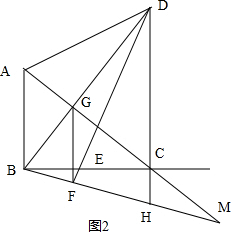
��GF��BCʱ����ʱGF��AB��CD��$\frac{BG}{GD}$=$\frac{AB}{CD}$=$\frac{1}{2}$
��ʱ$\frac{BG}{GD}$=$\frac{BF}{FH}$=$\frac{1}{2}$
�ߡ�BCH�ס�DCE
��$\frac{BH}{DE}$=$\frac{BC}{DC}$=$\frac{3}{6}$=$\frac{1}{2}$
��BF=$\frac{1}{3}$BH=$\frac{1}{6}$DE
���BFE�ס�DCE
��$\frac{BF}{DC}$=$\frac{BE}{DE}$
��$\frac{\frac{1}{6}DE}{6}$=$\frac{x}{DE}$
��DE2=36x=��3-x��2+62��
���x=21-6$\sqrt{11}$ ��x=21+6$\sqrt{11}$��3������ȥ��
�ڵ�E������BC��ʱ��ͼ3����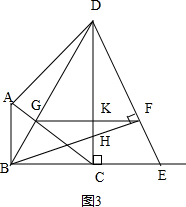
GF��DC��GF��BE����GF��CD����ΪK���ɢٿ�֪
$\frac{GK}{BC}$=$\frac{DG}{BD}$=$\frac{DK}{DC}$=$\frac{2}{3}$����GK=$\frac{2}{3}$��3=2��DK=4
��KF=a����$\frac{a}{3}$=$\frac{KH}{HC}$=$\frac{KH}{2-KH}$��
��KH=$\frac{2a}{3+a}$��HC=$\frac{6}{3+a}$��
�ߡ�BCD=��DKF=90��
���KDF=��CBH
��tan��KDF=tan��CBH
��$\frac{a}{4}$=$\frac{\frac{6}{3+a}}{3}$
���a=$\frac{-3+\sqrt{41}}{2}$��a=$\frac{-3-\sqrt{41}}{2}$��0����ȥ��
��$\frac{KF}{CE}$=$\frac{DK}{DC}$=$\frac{2}{3}$
��CE=$\frac{3}{2}$a=$\frac{-9+3\sqrt{41}}{4}$��BE=CE+3=$\frac{3+3\sqrt{41}}{4}$
���Ͽ�֪��x��ֵΪ21-6$\sqrt{11}$ ��$\frac{3+3\sqrt{41}}{4}$
���� ������Ҫ������ƽ���ߵȷ��߶ζ�����Ӧ�ú����������ε����Ʊ���Ϊ������ϵ�з��̽ⷽ�̵ķ�������1���и��������жϳ���BHDΪ�����������ǽ���Ĺؼ�����2��������Ҫ�����������������κ�ƽ���ߵȷ��߶ζ����еijɱ����߶���Ϊ������ϵ���õ�x��y֮��ĵ�����ϵ���������ɵõ�y����x�ĺ�����ϵʽ����3������Ҫ�Ǹ����߶�GF��ֱ������ABCD�е�һ���ߣ�AD���⣩��ֱʱ����������������ۣ�GF��BC��GF��DCʱ�ֱ��ж�Ӧ�����������Σ����������������еijɱ����߶���Ϊ������ϵ�з��̽ⷽ�̼��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
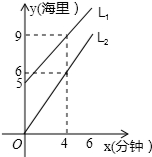 L1Ϊ��˽����L2Ϊ�ҹ�����ͧ������ʱ·����ʱ��ĺ���ͼ����ͼ��
L1Ϊ��˽����L2Ϊ�ҹ�����ͧ������ʱ·����ʱ��ĺ���ͼ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
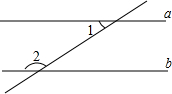 ��֪����ͼ����1�͡�2��ֱ��a��b��ֱ��c�س���ͬ���ڽǣ��ҡ�1���2��������֤��a��b��
��֪����ͼ����1�͡�2��ֱ��a��b��ֱ��c�س���ͬ���ڽǣ��ҡ�1���2��������֤��a��b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��Rt��ACB�У���ACB=90�㣬��A=15�㣬AB�Ĵ�ֱƽ������AC���ڵ�D����AB���ڵ�E������BD����AD=14����BC�ij�Ϊ��������
��ͼ��Rt��ACB�У���ACB=90�㣬��A=15�㣬AB�Ĵ�ֱƽ������AC���ڵ�D����AB���ڵ�E������BD����AD=14����BC�ij�Ϊ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
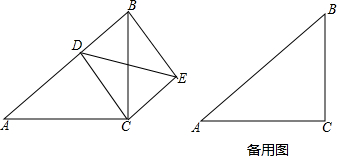
 ��ͼ��AC��BD�ཻ�ڵ�E��AD��BC����AE=2��CE=3��AD=3����BC�ij����ǣ�������
��ͼ��AC��BD�ཻ�ڵ�E��AD��BC����AE=2��CE=3��AD=3����BC�ij����ǣ�������| A�� | 2 | B�� | 3 | C�� | 4.5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com