
【题目】我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润![]() (万元).当地政府拟在“十三五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润
(万元).当地政府拟在“十三五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润![]() (万元).
(万元).
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2)该方案是否具有实施价值?
【答案】(1)205万元;(2)3175万元;(3)有
【解析】
(1)由获得利润与投入的函数关系式:![]() ,可得每年获得利润的最大值,从而可得答案;
,可得每年获得利润的最大值,从而可得答案;
(2)首先求得前两年的获利最大值,注意前两年:0≤x≤50,此时因为P随x的增大而增大,所以x=50时,P值最大;然后后三年:设每年获利y,设当地投资额为a,则外地投资额为100-a,即可得函数y=P+Q,整理求解即可求得最大值,则可求得按规划实施,5年所获利润(扣除修路后)的最大值;
(3)比较可知,该方案是具有极大的实施价值.
解:(1)当x=60时,P的最大值为41万元,
∴5年所获利润的最大值是:41×5=205(万元);
(2)前两年:0≤x≤50,此时因为P随x的增大而增大,
∴x=50时,P最大为:![]() (万元),
(万元),
后三年:设每年获利y,设当地投资额为a,则外地投资额为100﹣a,
∴![]()
![]() ,
,
![]()
![]()
∴当a=30时,y最大为1065,
∴这三年的获利最大为1065×3=3195(万元),
∴5年所获利润(扣除修路后)的最大值是:80+3195-50×2=3175(万元).
(3)有很大的实施价值.
规划后5年总利润为3175万元,不实施规划方案仅为205万元,故具有很大的实施价值.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
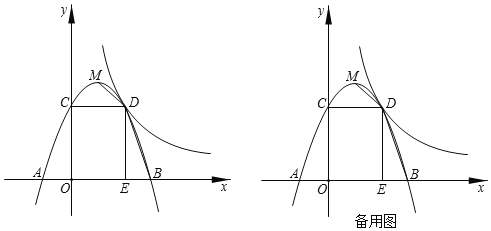
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线于另一点D,作DE⊥x轴,垂足为点E,双曲线y=![]() (x>0)经过点D,连接MD,BD.
(x>0)经过点D,连接MD,BD.
(1)求抛物线的表达式;
(2)点N,F分别是x轴,y轴上的两点,当以M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;
(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系![]() 中,等腰
中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,
轴上,![]() ,顶点
,顶点![]() 在
在![]() 的正半轴上,
的正半轴上,![]() ,一动点
,一动点![]() 从
从![]() 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿![]() 向左运动,到达
向左运动,到达![]() 的中点停止.另一动点
的中点停止.另一动点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向左运动,到达点
向左运动,到达点![]() 停止.已知点
停止.已知点![]() 、
、![]() 同时出发,以
同时出发,以![]() 为边作正方形
为边作正方形![]() ,使正方形
,使正方形![]() 和
和![]() 在
在![]() 的同侧.设运动的时间为
的同侧.设运动的时间为![]() 秒(
秒(![]() ).
).
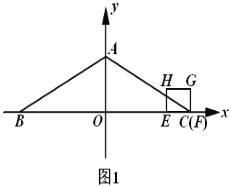
(1)当点![]() 落在
落在![]() 边上时,求
边上时,求![]() 的值;
的值;
(2)设正方形![]() 与
与![]() 重叠面积为
重叠面积为![]() ,请问是存在
,请问是存在![]() 值,使得
值,使得![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由;
值;若不存在,请说明理由;
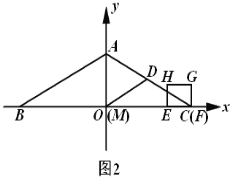
(3)如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() ,当点
,当点![]() 、
、![]() 开始运动时,点
开始运动时,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 运动,到达点
运动,到达点![]() 停止运动.请问在点
停止运动.请问在点![]() 的整个运动过程中,点
的整个运动过程中,点![]() 可能在正方形
可能在正方形![]() 内(含边界)吗?如果可能,求出点
内(含边界)吗?如果可能,求出点![]() 在正方形
在正方形![]() 内(含边界)的时长;若不可能,请说明理由.
内(含边界)的时长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
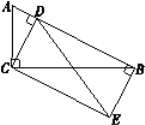
【题目】如图,在Rt△ABC中,![]() ,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
,CD⊥AB于点D,BE⊥AB于点B,BE=CD,连接CE,DE.
(1)求证:四边形CDBE为矩形;
(2)若AC=2,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
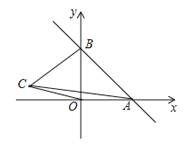
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() .
.![]() 轴,且与直线
轴,且与直线![]() 交于点
交于点![]() ,
,![]() 轴并交
轴并交![]() 轴于点
轴于点![]() ,点
,点![]() 是折线
是折线![]() 上一点.设过点
上一点.设过点![]() ,
,![]() 的直线为
的直线为![]() .
.
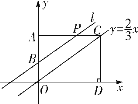
(1)点![]() 的坐标为________;若
的坐标为________;若![]() 所在的直线
所在的直线![]() 的函数值随
的函数值随![]() 的增大而减小,则
的增大而减小,则![]() 的取值范围是________;
的取值范围是________;
(2)当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)若![]() 与线段
与线段![]() 有交点,设该交点为
有交点,设该交点为![]() ,是否存在
,是否存在![]() 的情况?若存在,求点
的情况?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com