练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆来完成此项任务. 已知每辆甲种货车一次最多运送机器45台、租车费用400元，每辆乙种货车一次最多运送机器30台租车费用280元. 设租用甲种货车辆（为正整数）

    （1）请用含的代数式表示租车费用；

    （2）存在能完成此项运送任务的最节省费用的租车方案吗？若存在，请计算并给出租车方案；若不存在，请说明理由.

    【答案】(1);(2) 甲6辆，乙车2辆.

    【解析】（1）租甲种货车的费用为:,租乙种货车的费用为：，即可表示出租车费用.

    根据一次函数的性质回答即可.

    （1）

    ，

    解得

    因为的取值随着的增大而增大，

    所以当时，取得最小值，最小值为元,

    此时租车方案为：甲6辆，乙车2辆.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知：∠MON=30o，点A1、A2、A3 在射线ON上，点B1、B2、B3…．．在射线OM上，△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形，若OA1=l，则△A6B6A7 的边长为【 】

    A．6 B．12 C．32 D．64

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：点O到△ABC的两边AB、AC所在直线的距离相等，且OB＝OC。

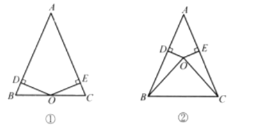
    （1）如图①，若点O在BC上，求证：AB＝AC；

    （2）如图②，若点O在△ABC的内部，上题的结论还成立吗？为什么？

    （3）若点O在△ABC的外部，AB＝AC成立吗？请画图表示。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个大小不同的等腰直角三角板如图1所示放置，图2是由它抽象出的几何图形，图中AB=AC，AD=AE，∠BAC=∠EAD=90°，B,C,E在同一条直线上，连结DC．

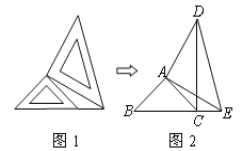
    （1）图2中的全等三角形是_______________,并给予证明（说明：结论中不得含有未标识的字母）；

    （2）指出线段DC和线段BE的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

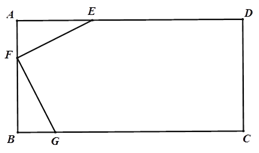
    【题目】如图，有一块矩形板材ABCD，AB=3米，AD=6米,E，F,G分别在AD,AB,BC上，∠EFG=900，EF=FG= 米，AF<BF.现想从此板材中剪出一个四边形EFGH,使得∠EHG=450，则四边形EFGH面

    积的最大值是____________平方米.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将四张边长各不相同的正方形纸片按如图方式放入矩形内(相邻纸片之间互不重叠也无缝隙)，未被四张正方形纸片覆盖的部分用阴影表示．设右上角与左下角阴影部分的周长的差为．若知道的值，则不需测量就能知道周长的正方形的标号为（ ）

    A.①B.②C.③D.④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，F为边AB的中点，DF与对角线AC交于点G，过点G作GE⊥AD于点E.若AB=2，且∠1=∠2，则下列结论：①DF⊥AB；②CG=2GA；③CG=DF+GE；④S四边形BFOC=.其中正确的有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

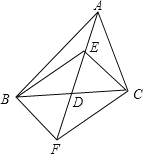
    【题目】在△ABC 中，D 是 BC 边的中点，E、F 分别在 AD 及其延长线上，CE∥BF，连接BE、CF．

    （1）求证：△BDF ≌△CDE；

    （2）若 DE =BC，试判断四边形 BFCE 是怎样的四边形，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（11·湖州）（本小题10分）

    如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。

    ⑴求证：四边形AECF是平行四边形；

    ⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。

    查看答案和解析>>

    同步练习册答案