
【题目】将四张边长各不相同的正方形纸片按如图方式放入矩形![]() 内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为
内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为![]() .若知道
.若知道![]() 的值,则不需测量就能知道周长的正方形的标号为( )
的值,则不需测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
科目:初中数学 来源: 题型:
【题目】如图1的矩形ABCD中,有一点E在AD上,今以BE为折线将A点往右折,如图2所示,再作过A点且与CD垂直的直线,交CD于F点,如图3所示,若AB=6![]() ,BC=13,∠BEA=60°,则图3中AF的长度为何?( )
,BC=13,∠BEA=60°,则图3中AF的长度为何?( )
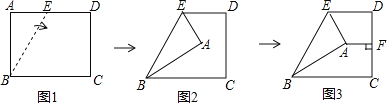
A. 2 B. 4 C. 2![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
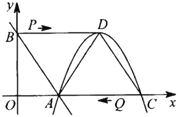
【题目】直线y=﹣![]() x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣
x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣![]() x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
(1)直接写出抛物线的解析式和点A,C,D的坐标;
(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
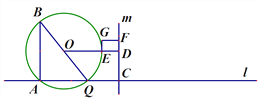
【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt![]() ,使∠BAQ=90°,
,使∠BAQ=90°,![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过![]() 的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆来完成此项任务. 已知每辆甲种货车一次最多运送机器45台、租车费用400元,每辆乙种货车一次最多运送机器30台租车费用280元. 设租用甲种货车![]() 辆(
辆(![]() 为正整数)
为正整数)
(1)请用含![]() 的代数式表示租车费用;
的代数式表示租车费用;
(2)存在能完成此项运送任务的最节省费用的租车方案吗?若存在,请计算并给出租车方案;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于点C,连接AD,OC.若△ABO的周长为![]() ,AD=2,则△ACO的面积为_________.
,AD=2,则△ACO的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
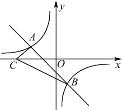
(1)求反比例函数和一次函数的解析式;
(2)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于未知数为 x,y 的二元一次方程组,如果方程组的解 x,y 满足![]() ,我们就说方程组的解 x 与 y 具有“邻好关系”.
,我们就说方程组的解 x 与 y 具有“邻好关系”.
(1) 方程组![]() 的解x与y是否具有“邻好关系”? 说明你的理由;
的解x与y是否具有“邻好关系”? 说明你的理由;
(2) 若方程组![]() 的解x与y具有“邻好关系”,求m的值;
的解x与y具有“邻好关系”,求m的值;
(3) 未知数为x,y的方程组![]() ,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
,其中a与x,y都是正整数,该方程组的解x与y是否具有“邻好关系”? 如果具有,请求出a的值及方程组的解;如果不具有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com