
【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
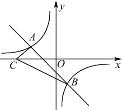
(1)求反比例函数和一次函数的解析式;
(2)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
【答案】(1)![]() ;y=-x-1;(2)
;y=-x-1;(2)![]() ;C(-5,0).
;C(-5,0).
【解析】
(1)将点B的坐标代入![]() 中求得m的值即可得到反比例函数的解析式,再将点A(-2,n)代入所得反比例函数的解析式求得n的值即可得到点A的坐标,然后将A、B两点的坐标代入一次函数的解析式列出关于k、b的方程组,解方程组求得k、b的值即可得到一次函数的解析式;
中求得m的值即可得到反比例函数的解析式,再将点A(-2,n)代入所得反比例函数的解析式求得n的值即可得到点A的坐标,然后将A、B两点的坐标代入一次函数的解析式列出关于k、b的方程组,解方程组求得k、b的值即可得到一次函数的解析式;
(2)如下图,作出点A关于x轴的对称点A′,连接BA′并延长交x轴于点C,则此时的点C为所求点,由已知条件求得直线BA′的解析式,即可由所得解析式求得点C的坐标,然后由t=CB-CA=CB-CA′即可求得所求的t的值.
(1)∵点B(1,-2)在反比例函数![]() 的图象上,
的图象上,
∴m=-2,
∴反比例函数解析式为![]() .
.
∵点A(-2,n)在反比例函数的图象上,
∴n=1,
∴A(-2,1).
由题意知![]() ,解得:
,解得:![]() ,
,
故一次函数的解析式为y=-x-1;
(2)如图,作点A关于x轴的对称点A′,连接BA′并延长交x轴于点C,则点C为所求点,

∵A(-2,1),
∴A′(-2,-1).
设直线A′B的解析式为y=mx+n,
则![]() ,解得:
,解得: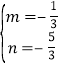 ,
,
故直线A′B的解析式为![]()
在![]() 中,令y=0,解得x=-5,则C点坐标为(-5,0),
中,令y=0,解得x=-5,则C点坐标为(-5,0),
∴BC=![]() ,A′C=
,A′C=![]() ,
,
∴此时t=CB-CA有最大值,且t最大=CB-CA′=A′B=![]() .
.


科目:初中数学 来源: 题型:
【题目】平价商场经销的甲、乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)甲种商品每件进价为 元,每件乙种商品利润率为 .
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元且“期间,该商场只对乙种商品进行如下的优惠促销活动:按下表优惠条件,
打折前一次性购物总金额 | 优惠措施 |
少于等于480元 | 不优惠 |
超过480元,但不超过680元 | 其中480元不打折,超过480元的部分给予6折优惠 |
超过680元 | 按购物总额给予7.5折优惠 |
若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将四张边长各不相同的正方形纸片按如图方式放入矩形![]() 内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为
内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示.设右上角与左下角阴影部分的周长的差为![]() .若知道
.若知道![]() 的值,则不需测量就能知道周长的正方形的标号为( )
的值,则不需测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家出发步行到公交站台后,等公交车去学校,如图, 折线表示这个过程中行程 s (千米)与所花时间 t (分)之间的关系,下 列说法错误的是( )
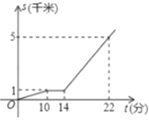
A.他家到公交车站台需行 1 千米B.他等公交车的时间为 4 分钟
C.公交车的速度是 500 米/分D.他步行与乘公交车行驶的平均速度300米/分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
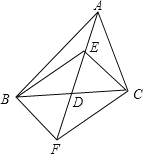
【题目】在△ABC 中,D 是 BC 边的中点,E、F 分别在 AD 及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF ≌△CDE;
(2)若 DE = BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
BC,试判断四边形 BFCE 是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC边上的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:

①AE=CF;②EF=AP;③2S四边形AEPF=S△ABC;④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)有BE+CF=EF;上述结论中始终正确的序号有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
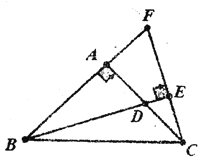
【题目】如图,等腰直角三角形ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△BDC的面积是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com