
【题目】平价商场经销的甲、乙两种商品,甲种商品每件售价98元,利润率为40%;乙种商品每件进价80元,售价128元.
(1)甲种商品每件进价为 元,每件乙种商品利润率为 .
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为3800元,求购进甲、乙两种商品各多少件?
(3)在“元且“期间,该商场只对乙种商品进行如下的优惠促销活动:按下表优惠条件,
打折前一次性购物总金额 | 优惠措施 |
少于等于480元 | 不优惠 |
超过480元,但不超过680元 | 其中480元不打折,超过480元的部分给予6折优惠 |
超过680元 | 按购物总额给予7.5折优惠 |
若小华一次性购买乙种商品实际付款576元,求小华在该商场购买乙种商品多少件?
【答案】(1)70,60%; (2)该商场购进甲种商品20件,乙种商品30件;(3)小华在该商场购买乙种商品5或6件.
【解析】
(1)根据商品利润率=![]() ×100%,可求每件乙种商品利润率,甲种商品每件进价;
×100%,可求每件乙种商品利润率,甲种商品每件进价;
(2)首先设出购进甲商品的件数,然后根据“同时购进甲、乙两种商品共50件”表示出购进乙商品的件数;然后根据“恰好用去3800元”列方程求出未知数的值,即可得解;
(3)分类讨论:小华一次性购买乙种商品超过480元,但不超过680元;超过680元,根据优惠条件分别计算.
(1)设甲种商品的进价为a元,则有:
98﹣a=40%a.
解得a=70.
即甲种商品每件进价为 70元,
![]() ×100%=60%,
×100%=60%,
即每件乙种商品利润率为 60%.
故答案是:70;60%;
(2)设该商场购进甲种商品x件,根据题意可得:
70x+80(50﹣x)=3800,
解得:x=20;
乙种商品:50﹣20=30(件).
答:该商场购进甲种商品20件,乙种商品30件.
(3)设小华在该商场购买乙种商品b件,
根据题意,得
①当过480元,但不超过680元时,480+(128b﹣480)×0.6=576
解得b=5.
②当超过680元时,128b×0.75=576
解得b=6.
答:小华在该商场购买乙种商品5或6件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图, AD 为△ ABC 的中线, BE 为△ ABD 的中线.

(1)∠ ABE=15°,∠ BED=55°,求∠ BAD 的度数;
(2)作△ BED 的边 BD 边上的高;
(3)若△ ABC 的面积为 20, BD=2.5,求△ BDE 中 BD 边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1的矩形ABCD中,有一点E在AD上,今以BE为折线将A点往右折,如图2所示,再作过A点且与CD垂直的直线,交CD于F点,如图3所示,若AB=6![]() ,BC=13,∠BEA=60°,则图3中AF的长度为何?( )
,BC=13,∠BEA=60°,则图3中AF的长度为何?( )
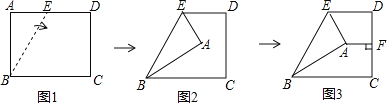
A. 2 B. 4 C. 2![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
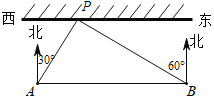
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE垂直平分AB.

(1)若AB=AC=10cm,BC=6cm,求△BCE的周长;
(2)若∠A=40°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
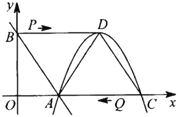
【题目】直线y=﹣![]() x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣
x+3交x轴于点A,交y轴于点B,顶点为D的抛物线y=﹣![]() x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
x2+2mx﹣3m经过点A,交x轴于另一点C,连接BD,AD,CD,如图所示.
(1)直接写出抛物线的解析式和点A,C,D的坐标;
(2)动点P在BD上以每秒2个单位长的速度由点B向点D运动,同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE=∠CAD时,求t的值;
②过点E作EM⊥BD,垂足为点M,过点P作PN⊥BD交线段AB或AD于点N,当PN=EM时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
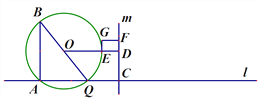
【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt![]() ,使∠BAQ=90°,
,使∠BAQ=90°,![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过![]() 的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
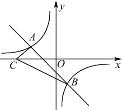
(1)求反比例函数和一次函数的解析式;
(2)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com