
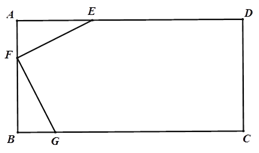
【题目】如图,有一块矩形板材ABCD,AB=3米,AD=6米,E,F,G分别在AD,AB,BC上,∠EFG=900,EF=FG=![]() 米,AF<BF.现想从此板材中剪出一个四边形EFGH,使得∠EHG=450,则四边形EFGH面
米,AF<BF.现想从此板材中剪出一个四边形EFGH,使得∠EHG=450,则四边形EFGH面
积的最大值是____________平方米.
【答案】![]()
【解析】根据余角的性质得到1=∠2,推出△AEF≌△BGF,根据全等三角形的性质得到![]() 接下来先证明四边形EFGO是正方形,求∠EOG的度数,得到四边形EFGH′是符合条件的最大四边形,根据矩形的面积公式即可得到结论.
接下来先证明四边形EFGO是正方形,求∠EOG的度数,得到四边形EFGH′是符合条件的最大四边形,根据矩形的面积公式即可得到结论.
能裁得,理由:
∵![]()
∴∠1=∠2.
在△AEF与△BGF中,
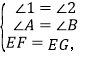
∴△AEF≌△BGF,
∴![]() 设
设![]() ,则
,则![]()
∴![]() 解得:x=1,x=2(不合题意,舍去).
解得:x=1,x=2(不合题意,舍去).
∴![]()
∴![]()
连接EG,作△EFG关于EG的对称△EOG,则四边形EFGO是正方形,∠EOG=90°.
以O为圆心,以OE为半径作⊙O,则使得∠EHG=45°的点在⊙O上.
连接FO,并延长交⊙O于H′,则H′在EG的垂直平分线上,连接EH′、GH′,则∠EH′G=45°,此时,四边形EFGH′是要想裁得符合要求的面积最大的四边形,
∴C在线段EG的垂直平分线上,
∴点F,O,H′,C在一条直线上.
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴OH′<OC,
∴点H′在矩形ABCD的内部.
∴可以在矩形ABCD中,裁得符合条件的面积最大的四边形EFGH′,
其面积=![]()
∴当所裁得的四边形为四边形EFGH′时,裁得了符合条件的最大四边形,其面积为(![]() )m2.
)m2.

故答案为:![]()


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B
(1)如图1,直接写出∠A和∠C之间的数量关系;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E.F在DM上,连接BE.BF.CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠ABF=2∠ABE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y1=![]() 与直线y2=ax+b交于点A(﹣4,1)和点B(m,﹣4).
与直线y2=ax+b交于点A(﹣4,1)和点B(m,﹣4).
(1)求双曲线和直线的解析式;
(2)直接写出线段AB的长和y1>y2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB=12,AC⊥AB,BD⊥AB,AC=BD=8。点P在线段AB上以每秒2个单位的速度由点A向点B运动,同时,点Q在线段BD上由B点向点D运动。它们的运动时间为t(s).
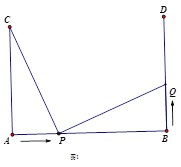

(1)若点Q的运动速度与点P的运动速度相等,当t=2时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图2,将图1中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变。设点Q的运动速度为每秒x个单位,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x,t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆来完成此项任务. 已知每辆甲种货车一次最多运送机器45台、租车费用400元,每辆乙种货车一次最多运送机器30台租车费用280元. 设租用甲种货车![]() 辆(
辆(![]() 为正整数)
为正整数)
(1)请用含![]() 的代数式表示租车费用;
的代数式表示租车费用;
(2)存在能完成此项运送任务的最节省费用的租车方案吗?若存在,请计算并给出租车方案;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8…顶点依次用A1,A2,A3,A4,…表示,则顶点A2019的坐标是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.8千克时,t的值为( )
A. 128B. 132C. 136D. 140
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD(请填空)

解:∵EF∥AD
∴∠2= (
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=70°( )
∴∠AGD= ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com