
【题目】如图,AB⊥EF,DC⊥EF,垂足分别为B、C,且AB=CD,BE=CF.AF、DE相交于点O,AF、DC相交于点N,DE、AB相交于点M.
(1)请直接写出图中所有的等腰三角形;
(2)求证:△ABF≌△DCE.
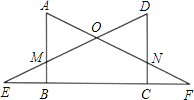
【答案】(1)△EOF,△AOM,△DON;(2)证明见解析
【解析】
(1)可以证明△ABF≌△DCE,根据全等三角形对应角相等可得∠A=∠D,∠DEC=∠AFB,所以△EOF是等腰三角形,再根据等角的余角相等可得∠A=∠AMO,∠D=∠DNO,从而得到△AOM与△DON也都是等腰三角形;
(2)由BE=CF,可以证明EC=BF,然后根据方法“边角边”即可证明△ABF与△DCE全等.
(1)解:△EOF,△AOM,△DON;
(2)证明:∵AB⊥EF于点B,DC⊥EF于点C,
∴∠ABC=∠DCB=90°,
∵CF=BE,
∴CF+BC=BE+BC,
即BF=CE…
在△ABF和△DCE中,
 ,
,
∴△ABF≌△DCE,


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
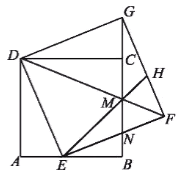
【题目】如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.
(1)求证:CD⊥CG;
(2)若tan∠MEN=![]() ,求
,求![]() 的值;
的值;
(3)已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
结果 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
两个正面 | 3 | 3 | 5 | 1 | 4 | 2 |
一个正面 | 6 | 5 | 5 | 5 | 5 | 7 |
没有正面 | 1 | 2 | 0 | 4 | 1 | 1 |
由上表结果,计算得出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是___________________.当试验组数增加到很大时,请你对这三种结果的可能性的大小作出预测:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BC均为等边三角形,连接AE、CD,PN、BF下列结论:①△ABE≌△DBC;②∠DFA=60°;③△BPN为等边三角形;④若∠1=∠2,则FB平分∠AFC.其中结论正确的有( )
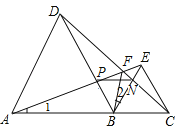
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
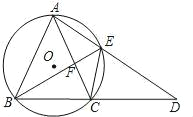
【题目】如图,△ABC内接于⊙O且AB=AC,延长BC至点D,使CD=CA,连接AD交⊙O于点E,连接BE、CE.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,EF=4,DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE.
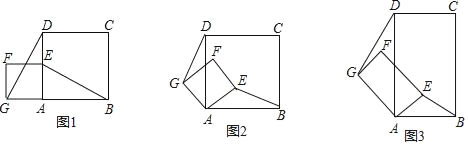
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ;②直线DG与直线BE之间的位置关系是 .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,AB=2,BC=5,∠MPN=90°,且∠MPN的直角顶点在BC边上,BP=1.
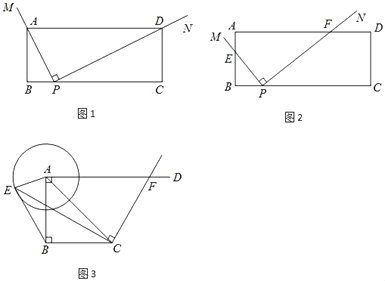
①特殊情形:若MP过点A,NP过点D,则![]() = .
= .
②类比探究:如图2,将∠MPN绕点P按逆时针方向旋转,使PM交AB边于点E,PN交AD边于点F,当点E与点B重合时,停止旋转.在旋转过程中,![]() 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
的值是否为定值?若是,请求出该定值;若不是,请说明理由.
(2)拓展探究:在Rt△ABC中,∠ABC=90°,AB=BC=2,AD⊥AB,⊙A的半径为1,点E是⊙A上一动点,CF⊥CE交AD于点F.请直接写出当△AEB为直角三角形时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com