
【题目】我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )
A. 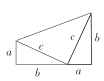 B.
B. 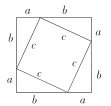 C.
C.  D.
D. 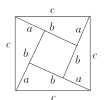
科目:初中数学 来源: 题型:
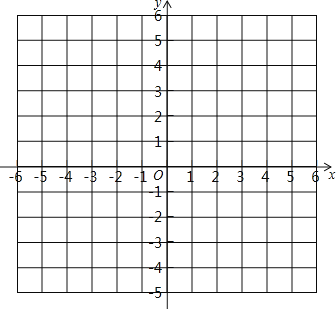
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某住宅小区在住宅建设时留下一块1798平方米的空地,准备建一个矩形的露天游泳池,设计如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带
(1)请你计算出游泳池的长和宽
(2)若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,请你计算要贴瓷砖的总面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点![]() 、
、![]() 、
、![]() ,请回答如下问题:
,请回答如下问题:
(1)在坐标系内描出点![]() 的位置:
的位置:
(2)求出以![]() 三点为顶点的三角形的面积;
三点为顶点的三角形的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10,若存在,请直接写出点
三点为顶点的三角形的面积为10,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
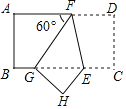
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且
且![]() ,GE=2BG,则折痕EF的长为( )
,GE=2BG,则折痕EF的长为( )
A. 4 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com