
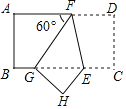
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且
且![]() ,GE=2BG,则折痕EF的长为( )
,GE=2BG,则折痕EF的长为( )
A. 4 B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】D
【解析】
由折叠的性质可知,DF=GF、HE=CE、GH=DC、∠DFE=∠GFE,结合∠AFG=60°即可得出∠GFE=60°,进而可得出△GEF为等边三角形.在Rt△GHE中,通过解含30度角的直角三角形及勾股定理即可得出GE=2EC、DC=![]() EC,再由GE=2BG结合矩形面积为8
EC,再由GE=2BG结合矩形面积为8![]() ,即可求出EC的长度,根据EF=GE=2EC即可求出结论.
,即可求出EC的长度,根据EF=GE=2EC即可求出结论.
由折叠的性质可知,DF=GF,HE=CE,GH=DC,∠DFE=∠GFE.
∵∠GFE+∠DFE=180°﹣∠AFG=120°,∴∠GFE=60°.
∵AF∥GE,∠AFG=60°,∴∠FGE=∠AFG=60°,∴△GEF为等边三角形,∴EF=GE.
∵∠FGE=60°,∠FGE+∠HGE=90°,∴∠HGE=30°.
在Rt△GHE中,∠HGE=30°,∴GE=2HE=2CE,∴GH=![]() =
=![]() HE=
HE=![]() CE.
CE.
∵GE=2BG,∴BC=BG+GE+EC=4EC.
∵矩形ABCD的面积为8![]() ,∴4EC
,∴4EC![]() EC=8
EC=8![]() ,∴EC=
,∴EC=![]() ,EF=GE=2
,EF=GE=2![]() .
.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
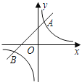
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当![]() 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲乙两所学校参赛人数相等,比赛结束后发现,学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表.
分数(分) | 人数(人) |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |

(1)在图一中80分所在的扇形的圆心角度数为
(2)请你将条形图补充完整
(3)求乙校成绩的平均分
(4)经计算知S2甲=135,S2乙=175,请你根据这两个数据,作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点以每秒2个单位长度的速度向左移动,
点以每秒2个单位长度的速度向左移动,
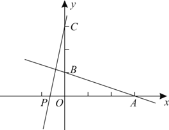
(1)求直线![]() 的表达式;
的表达式;
(2)求![]() 的面积
的面积![]() 与移动时间
与移动时间![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() ≌
≌![]() ,求出此时
,求出此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)______________.
(1)图象的对称轴是直线 x=1
(2)当x>1时,y随x的增大而减小
(3)一元二次方程ax2+bx+c=0的两个根是﹣1和3
(4)当﹣1<x<3时,y<0.
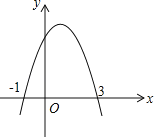
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com