
【题目】某住宅小区在住宅建设时留下一块1798平方米的空地,准备建一个矩形的露天游泳池,设计如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带
(1)请你计算出游泳池的长和宽
(2)若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,请你计算要贴瓷砖的总面积

【答案】(1)游泳池的长为50米,宽为25米.(2)要贴瓷砖的总面积是1700平方米.
【解析】
(1)可先设出游泳池的长和宽,然后根据条件表示出矩形空地的长和宽,然后根据矩形空地的面积是1798平方米来列方程求解.
(2)本题的关键是求出5个面的面积,有了(1)的长和宽,告诉了游泳池的高,可以用矩形的面积=长×宽计算出着5个面的面积,也就求出了贴瓷砖的面积.
解:(1)设游泳池的宽为x米,依题意得,
(x+6)(2x+8)=1798,
整理得x2+10x-875=0,
解得x1=25,x2=-35(负数不合题意,舍去),
所以x=25,2x=50.
答:游泳池的长为50米,宽为25米.
(2)(25+50)×2×3+25×50=1700(平方米).
答:要贴瓷砖的总面积是1700平方米.


科目:初中数学 来源: 题型:
【题目】某工厂,甲负责加工A型零件,乙负责加工B型零件.已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个.
(1)求甲、乙每天各加工多少个零件;
(2)根据市场预测估计,加工一个A型零件所获得的利润为35元/件,加工一个B型零件所获得的利润每件比A型少5元,现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于9850元,求至少应该生产多少个A型零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
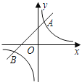
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当![]() 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 交x轴于A、B两点,交y轴于点C,顶点为D.
交x轴于A、B两点,交y轴于点C,顶点为D.

(1)写出抛物线的对称轴及C、D两点的坐标(用含a的代数式表示)
(2)连接BD并以BD为直径作⊙M,当a=-1时,请判断⊙M是否经过点C,并说明理由;
(3)在(2)题的条件下,点P是抛物线上任意一点,过P作直线垂直于对称轴,垂足为Q. 那么是否存在这样的点P,使△PQD与以B、C、D为顶点的三角形相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
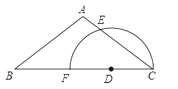
【题目】已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=![]() ,AE=1.求:
,AE=1.求:
(1)线段CD的长度;
(2)点A和点F之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com