
【题目】某工厂,甲负责加工A型零件,乙负责加工B型零件.已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个.
(1)求甲、乙每天各加工多少个零件;
(2)根据市场预测估计,加工一个A型零件所获得的利润为35元/件,加工一个B型零件所获得的利润每件比A型少5元,现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于9850元,求至少应该生产多少个A型零件?
【答案】(1)甲每天加工15个A型零件,乙每天加工20个B零件;(2)至少应该生产170个A型零件.
【解析】
(1)设甲每天加工x个零件,则乙每天加工(35﹣x)个零件,根据工作时间=工作总量÷工作效率结合甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设应该生产m个A型零件,则生产(300﹣m)个B型零件,根据总利润=单个利润×生产数量结合所获得的总利润不低于9850元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.
解:(1)设甲每天加工x个A型零件,则乙每天加工(35﹣x)个B型零件,
依题意,得:![]() =
=![]() ,
,
解得:x=15,
经检验,x=15是原方程的解,且符合题意,
∴35﹣x=20.
答:甲每天加工15个A型零件,乙每天加工20个B零件.
(2)设应该生产m个A型零件,则生产(300﹣m)个B型零件,
依题意,得:35m+(35﹣5)(300﹣m)≥9850,
解得:m≥170.
答:至少应该生产170个A型零件.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=-![]() x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x+6经过A、C两点.
x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x+6经过A、C两点.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,过点P作PQ∥AC,PQ交直线BC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,作点P关于直线AC的对称点点K,连接QK,当点K落在直线y=-![]() x上时,求线段QK的长.
x上时,求线段QK的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0)的图象与函数y=x-![]() 的图象如图所示,则下列结论:①ab>0;②c>-
的图象如图所示,则下列结论:①ab>0;②c>-![]() ;③a+b+c<-
;③a+b+c<-![]() ;④方程ax2+(b-1)x+c+
;④方程ax2+(b-1)x+c+![]() =0有两个不相等的实数根.其中正确的有( )
=0有两个不相等的实数根.其中正确的有( )
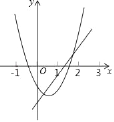
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .
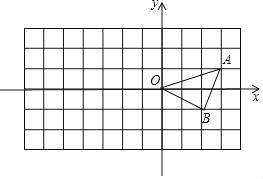
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=-1,有以下结论:①abc>0;②4ac<b2;③2a+b=0;④a-b+c>0.其中正确的结论的个数是( )
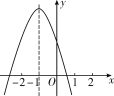
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1 上找一点M,使点M到点A的距离与到点C的距离之和最小,求点M的坐标.
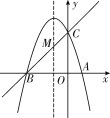
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 和
和![]() 中,
中,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.

(1)求证:![]()
(2)如图(2),若![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() . ①求
. ①求![]() 的度数;
的度数;
②若![]() 平分
平分![]() ,试说明:
,试说明:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某住宅小区在住宅建设时留下一块1798平方米的空地,准备建一个矩形的露天游泳池,设计如图所示,游泳池的长是宽的2倍,在游泳池的前侧留一块5米宽的空地,其它三侧各保留2米宽的道路及1米宽的绿化带
(1)请你计算出游泳池的长和宽
(2)若游泳池深3米,现要把池底和池壁(共5个面)都贴上瓷砖,请你计算要贴瓷砖的总面积

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com