
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D重合).
(1)当圆心O在∠BAD内部,∠ABO+∠ADO=50°时,∠A = °;
(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠C的度数;
(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.

【答案】⑴500;(2)1200;(3)|∠ABO﹣∠ADO|=60°
【解析】
(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠BAD=∠OAB+∠OAD=∠ABO+∠ADO=50°;
(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠BAD,则∠BCD=2∠BAD,然后根据圆内接四边形的性质由∠BCD+∠BAD =180°,易计算出∠BAD的度数,从而得出结论;
(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,所以∠ADO﹣∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO﹣∠ADO=60°.
(1)连接OA,如图1.
∵OA=OB,OA=OD.
∵∠OAB=∠ABO,∠OAD=∠ADO,∴∠BAD=∠OAB+∠OAD=∠ABO+∠ADO=50°;
(2)∵四边形OBCD为平行四边形,∴∠BOD=∠BCD.
∵∠BOD=2∠BAD,∴∠BCD=2∠BAD.
∵∠BCD+∠BAD =180°,即3∠BAD =180°,∴∠BAD =60°,∴∠C=180°-60°=120°;
(3)当∠OAB比∠ODA小时,如图2.
∵OA=OB,OA=OD.
∵∠OAB=∠ABO,∠OAD=∠ADO,∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,∴∠ADO﹣∠ABO=60°;
当∠OAB比∠ODA大时,同理可得∠ABO﹣∠ADO=60°.
综上所述:|∠ABO﹣∠ADO|=60°.


科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共20只,某学习小组作摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表示活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
请估算口袋中白球约是( )只.
A. 8 B. 9 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠DAB=∠CAE,AD=AB,AC=AE.

(1)求证△ABE≌△ADC;
(2)设BE与CD交于点O,∠DAB=30°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
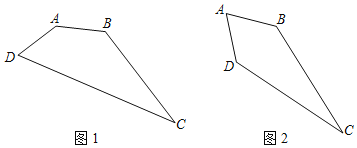
【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.如图1是一个四边形的木架,AB=AD=2cm,BC=5cm.
(1)扭动这个木架,四边形的形状就会改变,这说明了什么?
(2)如图2,若固定三根木条AB、BC、AD不动,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(3)在扭动这个木架过程中,当测得A、C之间的距离为6cm时,若CD的长度也是整数,那么CD的长应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]()
其中所有正确结论的序号是( )

A. ①②④ B. ①③④ C. ②③⑤ D. ①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.

![]() 根据“奇异三角形”的定义,小华提出命题“等边三角形一定是奇异三角形”是真命题还是假命题?
根据“奇异三角形”的定义,小华提出命题“等边三角形一定是奇异三角形”是真命题还是假命题?
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,若
,若![]() 是奇异三角形,求
是奇异三角形,求![]() .
.
![]() 如图,
如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点(不与点
上一点(不与点![]() 、
、![]() 重合),
重合),![]() 是半圆的中点,
是半圆的中点,![]() 、
、![]() 在直径
在直径![]() 的两侧,若在
的两侧,若在![]() 内存在点
内存在点![]() ,使
,使![]() ,
,![]() .
.
①求证:![]() 是奇异三角形;
是奇异三角形;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲 | 95 | 82 | 88 | 81 | 93 | 79 | 84 | 78 |
乙 | 83 | 92 | 80 | 95 | 90 | 80 | 85 | 75 |
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com