Question

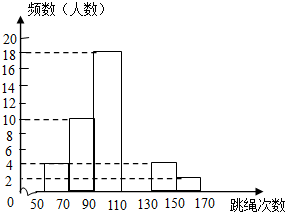
3．某中学为了了解七年级男生入学时的跳绳情况，随机选取50名刚入学的男生进行个人一分钟跳绳测试，并以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图（如图所示），根据图表解答下列问题：

组别	次数x	频数（人数）
第1组	50≤x＜70	2
第2组	70≤x＜90	a
第3组	90≤x＜110	18
第4组	110≤x＜130	b
第5组	130≤x＜150	4
第6组	150≤x＜170	2

（1）a=10，b14．
（2）若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀，则这50名男生中跳绳成绩为优秀的有多少人？优秀率为多少？
（3）若该校七年级入学时男生共有150人．请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数．

Answer 1

分析 （1）根据频数分布直方图可直接得到答案，利用50减去落在各小组的频数即可得到b；
（2）根据频数分布直方图可求得优秀的人数，然后根据$\frac{优秀人数}{总人数}$×100%求得优秀率．
（3）总人数×优秀率=七年级男生个人一分钟跳绳成绩为优秀的人数．

解答 解：（1）根据频数分布直方图知：a=10，
b=50-2-10-18-4-2=14．
故答案为10，14；

（2）成绩优秀的有：4+2=6（人），
优秀率为：$\frac{6}{50}$×100%=12%；

（3）150×12%=18（人）．
答：估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数为18人．

点评 此题主要考查读频数分布直方图的能力和利用统计图获取信息的能力．解题的关键是根据直方图得到进一步解题的有关信息．