练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知多项式（2ax2+3x-1）-（3x-2x2-3）的值与x无关，试求2a3-[a2-2（a+1）+a]-2的值．

    分析 已知多项式去括号合并得到最简结果，由结果与x无关求出a的值，原式去括号合并后代入计算即可求出值．

    解答 解：（2ax2+3x-1）-（3x-2x2-3）=2ax2+3x-1-3x+2x2+3=（2a+2）x2+2，
    由结果与x无关，得到2a+2=0，即a=-1，
    则原式=2a3-a2+2a+2-a-2=2a3-a2+a=-2-1-1=-4．

    点评 此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．已知3是关于x的方程$\frac{4}{3}$x2-2ax+1=0的一个解，则a的值是$\frac{13}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

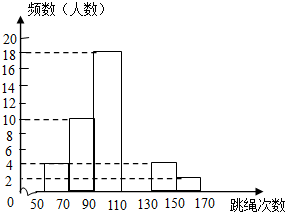    3．某中学为了了解七年级男生入学时的跳绳情况，随机选取50名刚入学的男生进行个人一分钟跳绳测试，并以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图（如图所示），根据图表解答下列问题：
    组别次数x频数（人数）
    第1组 50≤x＜702
    第2组 70≤x＜90a
    第3组 90≤x＜11018
    第4组 110≤x＜130b
    第5组 130≤x＜1504
    第6组 150≤x＜1702
    （1）a=10，b14．
    （2）若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀，则这50名男生中跳绳成绩为优秀的有多少人？优秀率为多少？
    （3）若该校七年级入学时男生共有150人．请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，四边形ABCD是正方形，E点在AB上，F点在BC的延长线上，且CF=AE，连接DE、DF、EF．
    ①求证：△ADE≌△CDF；
    ②填空：△CDF可以由△ADE绕旋转中心D点，按逆时针方向旋转90度得到；
    ③若BC=3，AE=1，求△DEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各数中最小的是（　　）
    A．23B．-32C．（-3）2D．（-2）3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算题
    （1）$\sqrt{3}$×$\sqrt{27}$    
    （2）$\frac{{\sqrt{32}}}{{\sqrt{2}}}$
    （3）（$\sqrt{2}$-1）（$\sqrt{2}$+1）
    （4）${（1-\sqrt{3}）^2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）$\sqrt{8}$-（π-$\frac{1}{2}$）0+$\root{3}{-64}$+|1-$\sqrt{2}$|
    （2）5x$\sqrt{xy}$÷3$\sqrt{\frac{y}{x}}$•$\frac{1}{3}$$\sqrt{\frac{x}{y}}$
    （3）（1-2$\sqrt{3}$）（1+2$\sqrt{3}$）-（2$\sqrt{3}$-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．若a，b互为相反数，c、d互为倒数，m的绝对值是1，求-3（a+b）-（cd）2014+m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．等边△ABC中，AO是BC边上的高，D为AO上一点，以CD为一边，在CD下方作等边△CDE，连接BE．
    （1）求证：△ACD≌△BCE；
    （2）过点C作CH⊥BE，交BE的延长线于H，若BC=8，求CH的长．

    查看答案和解析>>

    同步练习册答案