
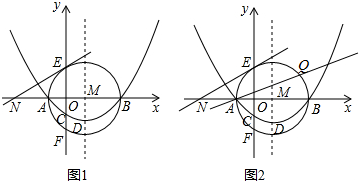
分析 (1)先证明△EOM是含有30度角的特殊三角形,得到OA=OM,进而求出点A、B坐标,利用待定系数法解决问题.
(2)不存在.如图1中,假设△PAB∽△BAD,过点P作PK⊥x轴存在为K,根据△PAK∽△DAM得到$\frac{PK}{DM}=\frac{AK}{AM}$列出方程,推出△PAB不是等腰三角形即可.
(3)如图2中,连接BQ,只要证明△AOH∽△AQB得$\frac{AH}{AB}=\frac{AO}{AQ}$即可解决问题.
解答 解:(1)如图1中连接EM.
∵NE是⊙O切线,∠ENM=30°,
∴ME⊥NE,
∴∠MEN=90°,
∴∠EMN=90°-∠ENM=60°,
在RT△EOM中,∵∠EMO=60°,
∴∠MEO=30°,
∴EM=2MO,
∴AM=2OM,
∴AO=OM,设AO=OM=m,
∵|x1-x2|=2,
∴4m=2,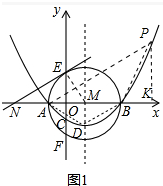
∴m=$\frac{1}{2}$,
∴A(-$\frac{1}{2}$,0),B($\frac{3}{2}$,0),
由题意:$\left\{\begin{array}{l}{\frac{1}{4}a-\frac{1}{2}b+c=0}\\{\frac{9}{4}a+\frac{3}{2}b+c=0}\\{c=-2}\end{array}\right.$解得$\left\{\begin{array}{l}{a=\frac{8}{3}}\\{b=-\frac{8}{3}}\\{c=-2}\end{array}\right.$,
∴抛物线的解析式为:y=$\frac{8}{3}{x}^{2}$-$\frac{8}{3}$x-2,顶点D($\frac{1}{2}$,-$\frac{8}{3}$).
(2)不存在.理由如下:
如图1中,假设△PAB∽△BAD,过点P作PK⊥x轴存在为K,设P(m,$\frac{8}{3}{m}^{2}$-$\frac{8}{3}$m-2),
∵∠PAK=∠MAD,∠PKA=∠DMA=90°,
∴△PAK∽△DAM,
∴$\frac{PK}{DM}=\frac{AK}{AM}$,
∴$\frac{\frac{8}{3}{m}^{2}-\frac{8}{3}m-2}{\frac{8}{3}}=\frac{m+\frac{1}{2}}{1}$,
∴m=$\frac{5}{2}$(或-$\frac{1}{2}$舍弃),
∴点P坐标为($\frac{5}{2}$,8),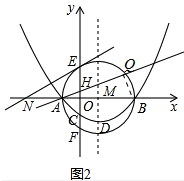
∵显然AB≠PB,而△ABD是等腰三角形,
∴不存在.
(3)结论:AH•AQ=1,理由如下:
如图2中,连接BQ,
∵AB是直径,
∴∠AQB=90°,
∵∠HAO=∠BAQ,∠HOA=∠AQB=90°,
∴△AOH∽△AQB,
∴$\frac{AH}{AB}=\frac{AO}{AQ}$,
∴AH•AQ=AO•AB=$\frac{1}{2}$•2=1.
点评 本题考查二次函数的有关知识、圆的性质、相似三角形的判定和性质等知识,解决问题的关键是找到特殊三角形这个突破口,学会利用相似三角形的性质,列出方程用方程的思想解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
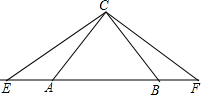 如图,已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=AC=2,求△ECF的面积.
如图,已知△ABC为等腰直角三角形,∠ACB=90°,延长BA至E,延长AB至F,∠ECF=135°,如果AE=AC=2,求△ECF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
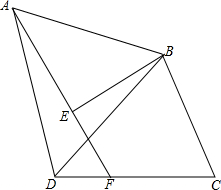 已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.
已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )| A. | 点M | B. | 点P | C. | 点Q | D. | 点N |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
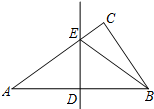 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=10,AC=8,则△BCE的周长是14.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=10,AC=8,则△BCE的周长是14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com