
分析 (1)利用完全平方公式易得7+2$\sqrt{10}$=($\sqrt{5}$+$\sqrt{2}$)2;
(2)利用完全平方公式求解;
(3)把等式右边展开即可得到m+n=a,mn=18,则利用整数的特征得到mn=1×18=2×9=3×6,于是可得m+n的值.
解答 解:(1)7+2$\sqrt{10}$=5+2+2$\sqrt{5×2}$=($\sqrt{5}$)2+2×$\sqrt{5}$×$\sqrt{2}$+($\sqrt{2}$)2=($\sqrt{5}$+$\sqrt{2}$)2;
(2)a+b-2$\sqrt{ab}$=($\sqrt{a}$-$\sqrt{b}$)2(a≥0,b≥0).
证明如下:左边=($\sqrt{a}$)2-2×$\sqrt{a}$×$\sqrt{b}$+($\sqrt{b}$)2=($\sqrt{a}$-$\sqrt{b}$)2=右边;
(3)∵($\sqrt{m}$$+\sqrt{n}$)2=m+n+2$\sqrt{mn}$,
∴m+n=a,mn=18,
而a、m、n均为正整数,
∴mn=1×18=2×9=3×6,
∴a=19或11或9.
故答案为$\sqrt{a}$-$\sqrt{b}$,19或11或9.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了完全平方公式.


科目:初中数学 来源: 题型:解答题
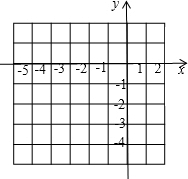 如图所示,已知△ABC是格点三角形
如图所示,已知△ABC是格点三角形查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
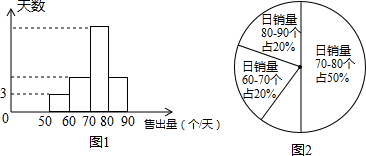
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | -$\sqrt{12}$ | D. | 6$\sqrt{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com