
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
分析 (1)销售出去的面包的盈利减去售不出去部分的亏损即可求出函数解析式;
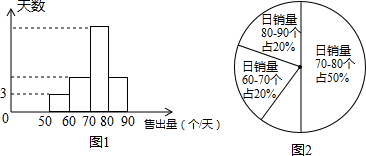
(2)①根据销售量是50-60个的天数是3,然后求得所占的百分比,据此即可求得m的值;
②求得当利润小于32元时,对应的天数,进而求解;
(3)利用加权平均数公式即可求解.
解答 解:(1)y=0.5x-0.3(80-x),即y=0.8x-24;
(2)①m=3÷(1-20%-20%-50%)=30;
②当y<32时,0.8x-24<32,
解得:x<70,
由图象可知,日销售量在60-70个的占20%,即30×20%=6,
则销售天数小于70时天数是:3+6=9(天).
(3)$\frac{70×1+72×2+73×3+75×4+78×3+79×2}{15}$=75.
即该组内平均每天销售面包的个数是75个.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)请用直尺和圆规确定已知圆的圆心,并作出此圆的内接正六边形ABCDEF;(保留作图痕迹,不写作法)
(1)请用直尺和圆规确定已知圆的圆心,并作出此圆的内接正六边形ABCDEF;(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,围棋盘的左下角呈现的是2015年3月7日韩国新人王战决赛第一局中的几手棋,为记录棋谱方便,横线用数字表示,竖线用英文字母表示,这样,黑棋①的位置可记为(C,4),白棋②的位置可记为(E,3),则黑棋⑨的位置应记为(D,6).
如图,围棋盘的左下角呈现的是2015年3月7日韩国新人王战决赛第一局中的几手棋,为记录棋谱方便,横线用数字表示,竖线用英文字母表示,这样,黑棋①的位置可记为(C,4),白棋②的位置可记为(E,3),则黑棋⑨的位置应记为(D,6).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
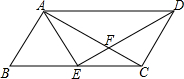 如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)
如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com