
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
分析 (1)根据等量关系:“2014年4月份用水20吨,交水费66元”;“5月份用水35吨,交水费150元”可列方程组求解即可.
(2)根据“当月的平均水费每吨不超过3.3元”,列出不等式求解即可.
解答 解:(1)根据题意,得:$\left\{\begin{array}{l}{17(a+0.8)+3(b+0.8)=66}\\{17(a+0.8)+13(b+0.8)+5×(6+0.8)=150}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2.2}\\{b=4.2}\end{array}\right.$.
答:a的值是2.2,b的值是4.2;
(2)设该户居民用水x吨,则
当x≤17时,a+0.8=3.
∵3<3.3
∴x>17
当17<x≤30时,17×3+5(x-17)=3.3x,
解得x=20.
当x>30时,不合题意.
答:该户居民用水量为20吨时,其当月的平均水费每吨为3.3元.
点评 本题考查一元一次不等式的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.同时考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题干找出合适的等量关系.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
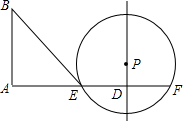 如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.
如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18 | B. | 32 | C. | 48 | D. | 72 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
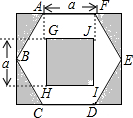 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC是格点三角形
如图所示,已知△ABC是格点三角形查看答案和解析>>
科目:初中数学 来源: 题型:选择题
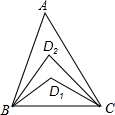 如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )| A. | 24° | B. | 25° | C. | 30° | D. | 36° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
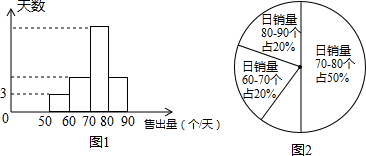
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com