
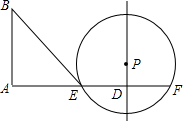
 如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.
如图,已知线段AD=10,过点D作PD⊥AD于D,点P是直线PD上一点,且PD=3,以点P为圆心,半径为5作⊙P交线段AD于点E及AD的延长线于点F,又过点A作BA⊥AD于A,BA=8,连接BE、PE.分析 (1)根据垂径定理得出ED=DF=$\frac{1}{2}$EF,根据勾股定理得出ED=4,即可求得EF;
(2)先证得△BAE∽△PDE,从而求得∠ABE=∠PED,进而证得∠PEB=90°,即PE⊥BE,即可证得直线BE与⊙P相切.
解答 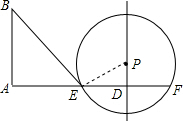 解:(1)∵PD⊥AD,点P为圆心,
解:(1)∵PD⊥AD,点P为圆心,
∴ED=DF=$\frac{1}{2}$EF,
连接PE,
在RT△PDE中,ED=$\sqrt{P{E}^{2}-P{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴EF=2ED=8;
(2)直线BE与⊙P相切;
∵AD=10,ED=4,
∴AE=10-4=6,
∵$\frac{BA}{AE}$=$\frac{8}{6}$=$\frac{4}{3}$,$\frac{ED}{PD}$=$\frac{4}{3}$,
∴$\frac{BA}{AE}$=$\frac{ED}{PD}$,
∵∠BAE=∠PDE=90°,
∴△BAE∽△PDE,
∴∠ABE=∠PED,
∵∠ABE+∠AEB=90°,
∴∠PED+∠AEB=90°,
∴∠PEB=90°,即PE⊥BE,
∴BE是⊙P的切线.
点评 此题考查了切线的判定,勾股定理,相似三角形的判定与性质,熟练掌握切线的判定是解本题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
 如图,小华画出了一次函数y=-3x-3的图象的一部分,根据图象解答下面的问题:
如图,小华画出了一次函数y=-3x-3的图象的一部分,根据图象解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.
在平行四边形ABCD中,BE⊥AD于点E,BF⊥CD于点F,若∠EBF=60°,且AE=2,DF=1,则EC的长为4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
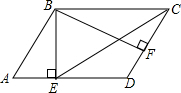
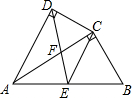 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com