
| A. | 18 | B. | 32 | C. | 48 | D. | 72 |
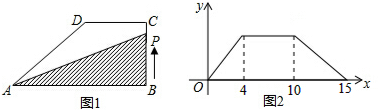
分析 根据图象可得BC=8,CD=20-8=12,DA=30-20=10,因为AB一定,即在三角形中底边一定,当高越大时面积越大,所以当点P在CD边上运动时,△ABP的面积最大.
解答 解:过点D作DE⊥AB,
则DE=BC=8,BE=CD=12
在Rt△ADE中,AE=$\sqrt{A{D}^{2}-A{E}^{2}}=\sqrt{1{0}^{2}-{8}^{2}}=6$
∴AB=8,S△ABP=$\frac{1}{2}$×AB×BC=$\frac{1}{2}$×18×8=72,即△ABP的最大面积为72.
故选D.
点评 此题考查动点函数问题,本题的关键是确定△ABP的面积最大时点P的位置.


科目:初中数学 来源: 题型:解答题
 在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
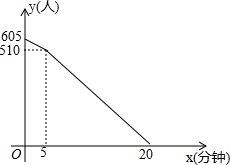 “五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题:
“五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
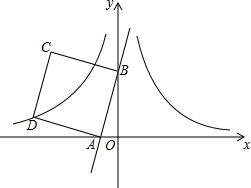 如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD.将过D点的双曲线y=$\frac{{k}_{1}}{x}$(x<0)沿y轴对折,得到双曲线y=$\frac{{k}_{2}}{x}$(x>0),将正方形ABCD沿x轴正方向向右平移a个单位长度后,点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$(x>0)上,则a的值是( )
如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD.将过D点的双曲线y=$\frac{{k}_{1}}{x}$(x<0)沿y轴对折,得到双曲线y=$\frac{{k}_{2}}{x}$(x>0),将正方形ABCD沿x轴正方向向右平移a个单位长度后,点C恰好也落在此双曲线y=$\frac{{k}_{2}}{x}$(x>0)上,则a的值是( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
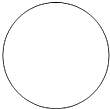 (1)请用直尺和圆规确定已知圆的圆心,并作出此圆的内接正六边形ABCDEF;(保留作图痕迹,不写作法)
(1)请用直尺和圆规确定已知圆的圆心,并作出此圆的内接正六边形ABCDEF;(保留作图痕迹,不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com