
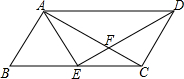
 如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)
如图,E是?ABCD的边BC的中点,AC⊥AB,∠B=60°.则下列结论中正确的是①②④.(把所有正确结论的序号都填在横线上)分析 由E是?ABCD的边BC的中点,AC⊥AB,根据直角三角形斜边的中线等于斜边的一半,可得AE=BE=CE=$\frac{1}{2}$BC,又由∠B=60°,可证得△ABE是等边三角形,即可证得AD=2AB;易求得∠CDA=∠B=60°,则可得DF平分∠ADC,由BE=CE,AD∥BC,可得S△ABE=S△DEC,然后由等高三角形的面积比等于对应底的比,求得S△ADE=$\frac{3}{2}$S△CDF;易得∠DAE=∠AEB=60°,∠ADE=30°,证得∠AED=90°.
解答 解:∵E是?ABCD的边BC的中点,AC⊥AB,
∴AE=BE=CE=$\frac{1}{2}$BC,
∵∠B=60°,
∴△ABE是等边三角形,
∴AB=BE,
∴BC=2AB;故①正确;
∵∠B=60°,
∴∠ECD=120°,
∵CE=CD,
∴∠CDE=30°,
∵∠CDA=∠B=60°,
∴DF平分∠ADC,故②正确;
∵BE=CE,AD∥BC,
∴S△ABE=S△DEC,
∵∠ACE=∠DEC=30°,
∴EF=CF,
∵AD∥BC,
∴△ADF∽△CEF,
∴CF:AF=EC:AD=1:2,
∴EF=CF=$\frac{1}{2}$AF,
∴S△CDF=$\frac{1}{2}$S△ADF,S△CDF=S△AEF,
∴S△ADE=$\frac{3}{2}$S△CDF;故③错误;
∵∠DAE=∠AEB=60°,∠ADE=30°,
∴∠AED=90°,
∴AE⊥DE,故④正确.
故答案为:①②④.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意相似三角形的对应边成比例以及等高三角形的面积比等于对应底的比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
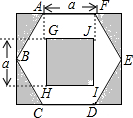 如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )
如图,某小区为增加居民的活动面积,将一块矩形空地设计为休闲区域,其中正六边形ABCDEF的顶点均在矩形边上,正六边形内部有一正方形GHIJ.根据设计,图中阴影部分种植草坪,则草坪面积为( )| A. | a2 | B. | ($\frac{\sqrt{3}}{2}$+1)a2 | C. | 2a2 | D. | $\frac{\sqrt{3}+1}{2}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
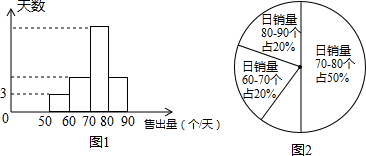
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
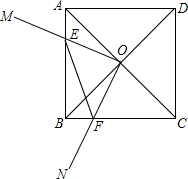 如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.
如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | -$\sqrt{12}$ | D. | 6$\sqrt{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com