
分析 设点O是△ABC的重心,连接AO,并延长AO交BC于点D,连接BO,并延长BO交CA于点E,连接CO,并延长CO交AB于点F,得到S△OBC=S△OCA=S△OAB,过点O作OG⊥BC于点G,OH⊥CA于点H,OG⊥AB于点I,得到BC=CA=AB,从而证得△ABC是正三角形.
解答 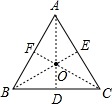 证明:不妨设点O是△ABC的重心,
证明:不妨设点O是△ABC的重心,
连接AO,并延长AO交BC于点D,
连接BO,并延长BO交CA于点E,
连接CO,并延长CO交AB于点F,
则AD,BE,CF分别是边BC,CA,AB上的中线,
∴S△ABD=S△ACD,S△OBD=S△OCD (等底同高的三角形面积相等),
∴S△ABD-S△OBD=S△ACD-S△OCD,
即S△AOB=S△AOC,
同理,可得:S△COA=S△COB,S△BOA=S△BOC,
即S△OBC=S△OCA=S△OAB,
过点O作OG⊥BC于点G,OH⊥CA于点H,OG⊥AB于点I,
∵点O是△ABC的内心,
∴OG=OH=OI,
∵OG,OH,OI分别是△OBC,△OCA,△OAB的高,
∴BC=CA=AB,
∴△ABC是正三角形.
点评 本题考查了三角形的无心,了解三角形的五心的性质是解答此类题目的难点和重点,本题难度较大,正确的作出辅助线是解答的关键.


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
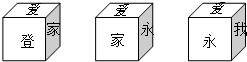 在立方体六个面上,分别标上“爱、我、家、乡、永、登”,如图是立体的三种不同摆法,则三种摆法的左侧面上三个字分别是( )
在立方体六个面上,分别标上“爱、我、家、乡、永、登”,如图是立体的三种不同摆法,则三种摆法的左侧面上三个字分别是( )| A. | 登、家、乡 | B. | 我、家、登 | C. | 我、登、家 | D. | 永、登、乡 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com