
【题目】如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
(1)当速度为50km/h、100km/h时,该汽车的耗油量分别为L/km、L/km.
(2)求线段AB所表示的y与x之间的函数表达式.
(3)速度是多少时,该汽车的耗油量最低?最低是多少?
【答案】
(1)0.13;0.14
(2)
解:由(1)得:线段AB的解析式为:y=﹣0.001x+0.18
(3)
解:设BC的解析式为:y=kx+b,
把(90,0.12)和(100,0.14)代入y=kx+b中得:
![]() 解得
解得 ![]() ,
,
∴BC:y=0.002x﹣0.06,
根据题意得 ![]() 解得
解得 ![]() ,
,
答:速度是80km/h时,该汽车的耗油量最低,最低是0.1L/km
【解析】解:(1)设AB的解析式为:y=kx+b,
把(30,0.15)和(60,0.12)代入y=kx+b中得:![]() 解得
解得 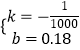
∴AB:y=﹣0.001x+0.18,
当x=50时,y=﹣0.001×50+0.18=0.13,
由线段BC上一点坐标(90,0.12)得:0.12+(100﹣90)×0.002=0.14,
故答案为:0.13,0.14;
本题考查了一次函数的应用,正确求出两线段的解析式是解好本题的关键,因为系数为小数,计算要格外细心,容易出错;另外,此题中求最值的方法:两图象的交点,方程组的解;同时还有机地把函数和方程结合起来,是数学解题方法之一,应该熟练掌握.(1)和(2):先求线段AB的解析式,因为速度为50km/h的点在AB上,所以将x=50代入计算即可,速度是100km/h的点在线段BC上,可由已知中的“该汽车的速度每增加1km/h,耗油量增加0.002L/km”列式求得,也可以利用解析式求解;(3)观察图形发现,两线段的交点即为最低点,因此求两函数解析式组成的方程组的解即可.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】禁渔期间,我渔政船在A处发现正北方向B处有一艘可以船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinαcosβ+cosαsinβ;sin(α﹣β)=sinαcosβ﹣cosαsinβ.例如sin90°=sin(60°+30°)=sin60°cos30°+cos60°sin30°= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =1.类似地,可以求得sin15°的值是 .
=1.类似地,可以求得sin15°的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.下列结论:
①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.
其中所有正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 ![]() MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( ) 
A.15
B.30
C.45
D.60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲乙两种商品,甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同.
(1)求甲、乙每个商品的进货单价;
(2)若甲、乙两种商品共进货100件,要求两种商品的进货总价不高于9000元,同时甲商品按进价提高10%后的价格销售,乙商品按进价提高25%后的价格销售,两种商品全部售完后的销售总额不低于10480元,问有哪几种进货方案?
(3)在条件(2)下,并且不再考虑其他因素,若甲乙两种商品全部售完,哪种方案利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com