练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠B＝42°，把△ABC绕着点A顺时针旋转，得到△AB'C'，点C的对应点C'落在BC边上，且B'A∥BC，则∠BAC'的度数为（　　）

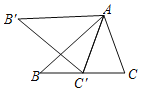
    A.24°B.25°C.26°D.27°

    【答案】D

    【解析】

    由旋转的性质得出∠B'＝∠B＝42°，∠AC'B'＝∠C，AC'＝AC，由AC'＝AC得出∠AC'C＝∠C＝∠AC'B'，由B'A∥BC得出∠B'C'C＝138°，求出∠AC'C＝∠C＝∠AC'B='69°，再由三角形的外角性质即可得出答案．

    解：由旋转的性质得：∠B'＝∠B＝42°，∠AC'B'＝∠C，AC'＝AC，

    ∴∠AC'C＝∠C＝∠AC'B'，

    ∵B'A∥BC，

    ∴∠B'+∠B'C'C＝180°，

    ∴∠B'C'C＝180°﹣42°＝138°，

    ∴∠AC'C＝∠C＝∠AC'B'＝×138°＝69°，

    ∴∠BAC'＝∠AC'C﹣∠B＝69°﹣42°＝27°；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

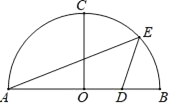
    【题目】如图，AB是半圆O的直径，半径OC⊥AB，OB＝4，D是OB的中点，点E是弧BC上的动点，连接AE，DE．

    （1）当点E是弧BC的中点时，求△ADE的面积；

    （2）若 ，求AE的长；

    （3）点F是半径OC上一动点，设点E到直线OC的距离为m，当△DEF是等腰直角三角形时，求m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料一：把一个自然数的个位数字截太再用余下的数加上个位数的4倍，如果和是13的倍数，则原数能被13整除．如果和太大不易看出是否13的倍数，可重复上述「截尾、倍大、相加、验和」的过程，直到能清楚判断为止．例如，判断377是否13的倍数的过程如下：37+7×4＝65，65÷13＝5，所以，377是13的倍数；又例如判断8632是否13的倍数的过程如下：863+2×4＝871，87+1×4＝91，91÷13＝7．所以，8632是13的倍数．

    材料二：若一个四位自然数n，满足千位与个位相同，百位与十位相同，我们称这个数为“对称数”．将“对称数”n的前两位与后两位交换位置得到一个新的n′，记F（n）＝，例如n＝3113，n′＝1331，（3113）＝＝18．

    （1）请用材料一的方法判断1326与3366能否被13整除；

    （2）若m、p是“对称数”，其中m＝ ，p＝（0≤b＜a≤5，1≤c＜a≤5且a，b，c均为整数），若m能被l3整除，且F（m）﹣F（p）＝36，求p．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，对往年的市场行情和生产情况进行了调查，提供了如下两个信息图，如甲、乙两图.

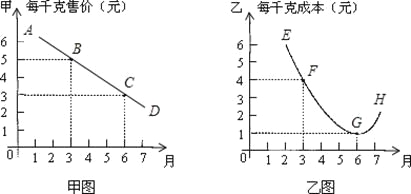
    注：甲、乙两图中的A，B，C，D，E，F，G，H所对应的纵坐标分别指相应月份每千克该种蔬菜的售价和成本（生产成本6月份最低，甲图的图象是线段，乙图的图象是抛物线的一部分）.请你根据图象提供的信息说明：

    （1）在3月份出售这种蔬菜，每千克的收益是多少元?（收益=售价-成本）

    （2）哪个月出售这种蔬菜，每千克的收益最大?说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点在抛物线上，且抛物线与轴分别交于点和点，与轴交于点

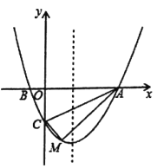
    （1）求抛物线的解析式.

    （2）若点为抛物线对称轴上的一个动点，求的最小值.

    （3）点为抛物线上除点外的一点，若与的面积相等，求点的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB＝120°，OC平分∠AOB，∠MCN＝60°，CM与射线OA相交于M点，CN与直线BO相交于N点．把∠MCN绕着点C旋转．

    （1）如图1，当点N在射线OB上时，求证：OC＝OM+ON；

    （2）如图2，当点N在射线OB的反向延长线上时，OC与OM，ON之间的数量关系是　 　（直接写出结论，不必证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“互联网+”时代，网上购物备受消费者青睐．某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可销售100条．为了吸引更多顾客，该网店采取降价措施．据市场调查反映：销售单价每降1元，则每月可多销售5条．设每条裤子的售价为元(为正整数)，每月的销售量为条．

    (1)直接写出与的函数关系式；

    (2)设该网店每月获得的利润为元，当销售单价降低多少元时，每月获得的利润最大，最大利润是多少？

    (3)该网店店主热心公益事业，决定每月从利润中捐出200元资助贫困学生．为了保证捐款后每月利润不低于4220元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2+2（m﹣1）x+m2﹣3＝0有两个不相等的实数根．

    （1）求m的取值范围；

    （2）若m为非负整数，且该方程的根都是无理数，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

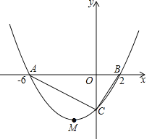
    【题目】如图所示，抛物线的顶点为，与轴交于、两点，且，与轴交于点．

    求抛物线的函数解析式；

    求的面积；

    能否在抛物线第三象限的图象上找到一点，使的面积最大？若能，请求出点的坐标；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案