
【题目】如图1,AB//EF,∠2=2∠1

(1)证明∠FEC=∠FCE;
(2)如图2,M为AC上一点,N为FE延长线上一点,且∠FNM=∠FMN,则∠NMC与∠CFM有何数量关系,并证明.
【答案】(1)见解析;(2)∠CFM=2∠NMC,理由见解析
【解析】
(1)由平行线的性质可得∠1=∠CEF,再加上∠2=2∠1,∠2=∠CEF+∠C,从而得到结论;
(2)如图,由三角形外角性质可得∠7=∠3+∠4,从而得到∠C=∠3+∠4,再加上∠C+∠5=∠8+∠N可得∠3+∠4+∠5=∠8+∠N,再加上∠FNM=∠FMN可得:∠3+∠4+∠5=∠8+∠3+∠8,从而得出结论.
(1)∵AB//EF,
∴∠1=∠CEF,
又∵∠2=2∠1(已知),∠2=∠CEF+∠C(三角形外角的性质),
∴2∠1=∠2=∠1+∠C,
∴∠1=∠C,
∴∠FEC=∠C,即∠FEC=∠FCE;
(2)如图所示:
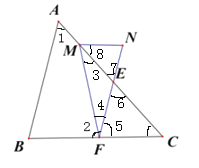
∵∠7=∠3+∠4,∠7=∠6,∠6=∠C(已证),
∴∠C=∠3+∠4,
又∵∠7=∠6,
∴∠C+∠5=∠8+∠N,
∴∠3+∠4+∠5=∠8+∠N,
又∵∠FNM=∠FMN,
∴∠N=∠3+∠8,
∴∠3+∠4+∠5=∠8+∠3+∠8,
又∵∠4+∠5=∠CFM,
∴∠3+∠CFM=∠8+∠3+∠8,
∴∠CFM=2∠8,即∠CFM=2∠NMC.


科目:初中数学 来源: 题型:
【题目】阅读材料:基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时,等号成立.其中我们把
(a>0,b>0),当且仅当a=b时,等号成立.其中我们把![]() 叫做正数a、b的算术平均数,
叫做正数a、b的算术平均数,![]() 叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
叫做正数a、b的几何平均数,它是解决最大(小)值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() 即是x+
即是x+![]() ≥2
≥2![]()
∴x+![]() ≥2
≥2
当且仅当x=![]() 即x=1时,x+
即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题
(1)若x>0,函数y=2x+![]() ,当x为何值时,函数有最小值,并求出其最小值.
,当x为何值时,函数有最小值,并求出其最小值.
(2)当x>0时,式子x2+1+![]() ≥2成立吗?请说明理由.
≥2成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级某班部分学生植树,若每人平均植树8棵,还剩7棵;若每人植树9棵,则有一名学生植树的棵树多于3棵而小于6棵.若设学生人数为x人,则植树棵树为(8x7)人,则下面给出的不等式(组)中,能准确求出学生人数与种植树木数量的是( )
A.8x769(x1)B.8x739(x1)
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是两张形状、大小相同但是画面不同的图片,把两张图片从中间剪断,再把四张形状相同的小图片(标注a、b、c、d)混合在一起,从四张图片中随机摸取一张,接着再随机摸取一张,则这两张小图片恰好合成一张完整图片的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AB=8,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边作等边△CEF,连接DF,则线段DF的最小值为( )

A.![]() B.4C.2D.无法确定
B.4C.2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小带根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况.
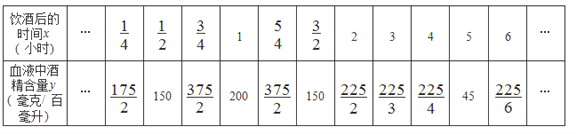
下面是小带的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,以上表中各对数值为坐标描点,图中已给出部分点,请你描出剩余的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线![]() 两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;

(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完250毫升低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
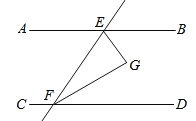
【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的点E处,折痕为PQ.过点E作EF∥AB交PQ于点F,连接BF

(1)若AP: BP=1:2,则AE的长为 .
(2)求证:四边形BFEP为菱形;
(3)当点E在AD边上移动时,折痕的端点P、Q也随之移动.若限定点P,Q分别在边AB、BC上移动,求出点E在边AD上移动的最大距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com