
如图是二次函数y=ax2+bx+c图像的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc>0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(2.5,y2)是抛物在线两点,则y1>y2,其中正确的是( )
| A.② | B.②③ | C.②④ | D.①② |
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:单选题
已知 的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
A. | B. | C. | D.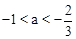 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0,你认为其中正确信息的个数有( )
| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
矩形OABC在平面直角坐标系中的位置如图所示,OA=3,AB=2.抛物线y=ax2+bx+c(a≠0)经过点A和点B,与x轴分别交于点D、E(点D在点E左侧),且OE=1,则下列结论:①a>0;②c>3;③2a﹣b=0;④4a﹣2b+c=3;⑤连接AE、BD,则S梯形ABDE=9.
其中正确结论的个数为( )
A. 1个 B.2个 C.3 个 D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图:点P(x,y)为平面直角坐标系内一点,PB⊥x 轴,垂足为B, A为(0,2),若PA=PB,则以下结论正确的是( ).
A.点P在直线 上 上 | B.点P在抛物线 上 上 |
C.点P在抛物线 上 上 | D.点P在抛物线 上 上 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
| A.13 | B.14 | C.15 | D.16 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,下列说法正确的是( )
| A.有最小值-5、最大值0 |
| B.有最小值-3、最大值6 |
| C.有最小值0、最大值6 |
| D.有最小值2、最大值6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com