
(本题满分12分)(1)阅读合作学习内容,解答其中的问题;
合作学习 如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数
①该反比例函数的解析式是什么? ②当四边形AEGF为正方形时,点F的坐标是多少? |
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由。
(1) ①y=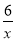 ②F(3,2)(2)不能全等 能相似 相似比为
②F(3,2)(2)不能全等 能相似 相似比为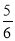
【解析】
试题分析:(1)根据矩形的性质和反比例函数的特点可以求出函数的解析式;再根据正方形的性质和反比例函数的特点求出F点的坐标;
(2)先假设全等,然后判断出F点不在反比例函数的图像上,判断出不全等;假设相似,得到相似的成比例线段,结合矩形的特点设出F点的坐标,根据反比例函数求出点F,从而求出相似比.
试题解析:(1)①∵四边形ABOD为矩形,EH⊥x,而OD=3,DE=2
∴E点的坐标为(2,3)
∴k=2×3=6
∴反比例函数的解析式为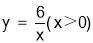
②设正方形AEGF的边长为a,则AE=AF=a
∴B点的坐标为(2+a,0),A点的坐标为(2+a,3)
∴F点的坐标为(2+a,3-a)
把F点代入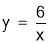 ,可得(2+a)(3-a)=6,
,可得(2+a)(3-a)=6,
解得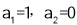 (舍去)
(舍去)
∴F点的坐标为(3,2)
(2)①当AE>EG时,矩形AECF与矩形DOHE不能全等.
理由:假设两矩形全等,则AE=OD=3,AF=DE=2,
∴A点的坐标为(5,3)
∴F点的坐标为(3,3)
而3×3=9≠6,F点不在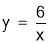 上
上
故矩形AECF与矩形DOHE不能全等
②当AE>EG时,若矩形AECF与矩形DOHE相似,根据相似的性质可得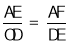
∴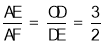 ,
,
设AE=3t,则AF=2t,得F点的坐标为(2+3t,3-2t),
所以由反比例函数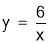 可得(2+3t)(3-2t)=6,
可得(2+3t)(3-2t)=6,
解得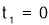 (舍去),
(舍去),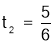
∴AE=3t=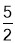 ,
,
∴相似比为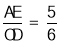
考点:反比例函数,矩形的性质,坐标与图形,矩形的相似


科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片九年级上学期期中考试数学试卷(解析版) 题型:填空题
已知圆内一点P到圆上各点的距离中最短距离为2cm,最长距离为8cm,则过P点的最短弦长为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列方程中,是一元二次方程的有( )
① ②
② ③
③ ④
④ 
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市姜堰区八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在Rt△ABC中,∠ACB=90°,E是AB上一点,且BE=BC,DE⊥AB于E,若AC=8,则AD+DE等于( )

A.7 B.8 C.9 D.10
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰兴市七年级上学期期中考试数学试卷(解析版) 题型:填空题
已知一直角三角形的木板,三边的平方和为7200 cm2,则斜边长为_______ cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰兴市七年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分)△ABC中,∠ACB=90°,AC=BC,AB=2.现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线AC、直线BC相交于点E、F.我们把DE⊥AC时的位置定为起始位置(如图1),将三角板绕点D顺时针方向旋转一个角度α (0°<α<90°).

(1)在旋转过程中,当点E在线段AC上,点F在线段BC上时(如图2),
①试判别△DEF的形状,并说明理由;
②判断四边形ECFD的面积是否发生变化,并说明理由.
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形?若存在,求出CG的长,若不存在,说明理由;



查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片七年级上学期期中考试数学试卷 题型:解答题
(本题5分)画一条数轴,然后在数轴上表示下列各数: ,
, ,
, ,并用“<”号把这些数连接起来.
,并用“<”号把这些数连接起来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com