
【题目】依据我市出租汽车运价与燃料(天然气)价格联动机制,经市政府同意,从2016年11月1日起,市区出租汽车每乘次起步价降低0.5元(不含非用天然气出租车).即排气量1.8L(含1.8L)以下车型由现行起步价3公里9元降低至3公里8.5元;超过3公里每公里运价为2.0元/公里;空驶补贴费为单程载客12公里以上的部分,每公里加收公里运价的50%.
(1)请写出新运价标准下乘车费用y元与乘车距离x公里之间的函数关系式;
(2)小明从家乘车去学校花费了10元,求他家与学校之间的距离是多少公里?
【答案】(1) ;(2)3.75公里
;(2)3.75公里
【解析】
(1)分0<x≤3、3<x≤12和x>12三种情况分析,当0<x≤3时,y值为起步价;当3<x≤12时,根据乘车费用=起步价+2×超出3公里的路程,即可得出y与x之间的函数关系式;当x>12时,根据乘车费用=起步价+2×(12﹣3)+2×(1+50%)×超出12公里的路程,即可得出y与x之间的函数关系式.综上即可得出结论;
(2)求出当x=12时,y=26.5,由8.5<10<26.5,可知3<x<12,再令y=2x+2.5=10,求出x的值即可.
解:(1)当0<x≤3时,y=8.5;
当3<x≤12时,y=8.5+2(x﹣3)=2x+2.5;
当x>12时,y=8.5+2×(12﹣3)+2×(1+50%)(x﹣12)=3x﹣9.5.
综上所述:新运价标准下乘车费用y元与乘车距离x之间的函数关系式为:
 ;
;
(2)当x=12时,y=2x+2.5=26.5,
∵8.5<10<26.5,
∴3<x<12.
当y=2x+2.5=10时,x=3.75.
答:小明家与学校之间的距离是3.75公里.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,将一块等腰直角三角形的直角顶点放在斜边
,将一块等腰直角三角形的直角顶点放在斜边![]() 的中点
的中点![]() 处,将三角板绕点
处,将三角板绕点![]() 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线![]() 、
、![]() 于
于![]() 、
、![]() 两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
两点.如图①、②、③是旋转三角板得到的图形中的3种情况.
(1)观察图①,当三角板绕点![]() 旋转到
旋转到![]() 时,我们发现:
时,我们发现:![]() __________
__________![]() .(选填“
.(选填“![]() ”、“
”、“![]() ”或“
”或“![]() ”)
”)
(2)当三角板绕点![]() 旋转到图②所示位置时,判断(1)题中
旋转到图②所示位置时,判断(1)题中![]() 与
与![]() 之间的大小关系还存在吗?请你结合图②说明理由.
之间的大小关系还存在吗?请你结合图②说明理由.
(3)三角板绕点![]() 旋转,
旋转,![]() 是否能成为等腰三角形?若能,指出所有情况(那写出
是否能成为等腰三角形?若能,指出所有情况(那写出![]() 为等腰三角形时
为等腰三角形时![]() 的长);若不能,请说明理由.
的长);若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
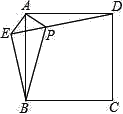
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程y(千米)与时间x(小时)的关系.根据图象,回答下列问题:

(1)B出发时与A相距 千米.
(2)B骑车一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程y与时间x的函数关系式.(写出过程)
(5)若B的自行车不发生故障,保持出发时的速度匀速行驶,A,B肯定会提前相遇.在图中画出这种假设情况下B骑车行驶过程中路程y与时间x的函数图象,在图中标出这个相遇点P,并回答相遇点P离B的出发点O相距多少千米.(写出过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com