
【题目】如图,利用热气球探测器测量大楼AB的高度,从热气球P处测得大楼B的俯角为37°,大楼底部A的俯角为60°,此时热气球P离底面的高度为120m.试求大楼AB的高度(结果保留整数).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.


(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角: ;所有与∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度数;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,分别探讨下面三个图形中∠AEC与∠EAB,∠ECD之间的关系,请你从所得到的关系中任选一个加以证明.

(1)在图1中,∠AEC与∠EAB,∠ECD之间的关系是:________________.
(2)在图2中,∠AEC与∠EAB,∠ECD之间的关系是:________________.
(3)在图3中,∠AEC与∠EAB,∠ECD之间的关系是:________________.
(4)在图______中,求证:________________.(并写出完整的证明过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△AFD为等腰直角三角形,∠FAD=∠BAC=90°,点D在BC上,则:
(1)求证:BF=DC.
(2)若BD=AC,则求∠BFD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.
(1)计算AB边的长等于;
(2)在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使矩形的面积等于△ABC的面积,并简要说明画图的方法(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据我市出租汽车运价与燃料(天然气)价格联动机制,经市政府同意,从2016年11月1日起,市区出租汽车每乘次起步价降低0.5元(不含非用天然气出租车).即排气量1.8L(含1.8L)以下车型由现行起步价3公里9元降低至3公里8.5元;超过3公里每公里运价为2.0元/公里;空驶补贴费为单程载客12公里以上的部分,每公里加收公里运价的50%.
(1)请写出新运价标准下乘车费用y元与乘车距离x公里之间的函数关系式;
(2)小明从家乘车去学校花费了10元,求他家与学校之间的距离是多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11
【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
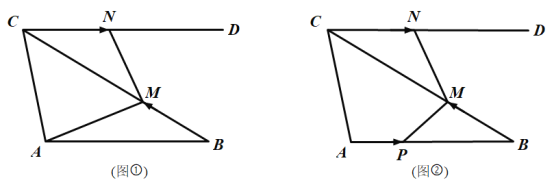
【题目】如图①,在![]() 中,
中,![]() cm ,
cm ,![]() cm,过点
cm,过点![]() 作射线
作射线![]() .点
.点![]() 从点
从点![]() 出发,以3 cm/s的速度沿
出发,以3 cm/s的速度沿![]() 匀速移动;点
匀速移动;点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿
cm/s的速度沿![]() 匀速移动.点
匀速移动.点![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止移动.连接
同时停止移动.连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() (s).
(s).
(1)点![]() 、
、![]() 从移动开始到停止,所用时间为 s;
从移动开始到停止,所用时间为 s;
(2)当![]() 与
与![]() 全等时,
全等时,
①若点![]() 、
、![]() 的移动速度相同,求
的移动速度相同,求![]() 的值;
的值;
②若点![]() 、
、![]() 的移动速度不同,求
的移动速度不同,求![]() 的值;
的值;
(3)如图②,当点![]() 、
、![]() 开始移动时,点
开始移动时,点![]() 同时从点
同时从点![]() 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿![]() 向点
向点![]() 匀速移动,到达点
匀速移动,到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 返回.当点
返回.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 、
、![]() 同时停止移动.在移动的过程中,是否存在
同时停止移动.在移动的过程中,是否存在![]() 与
与![]() 全等的情形?若存在,求出
全等的情形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com