
【题目】如图,已知ADBC,BC,垂足分别为D、F,23180,试说明:GDCB,请补充说明过程,并在括号内填上相应的理由。
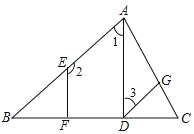
解:ADBC,EFBC(已知)
ADBEFB90( ① ),
EF//AD( ② ),
③ 2180( ④ ),
又23180(已知),
13( ⑤ ),
AB// ⑥ ( ⑦ ),
∴∠GDC=∠B( ⑧ )
【答案】垂直的定义;同位角相等,两直线平行;∠1,两直线平行,同旁内角互补;同角的补角相等;DG;内错角相等,两直线平行;两直线平行,同位角相等.
【解析】
根据平行线的判定与性质解答,先证明EF//AD,再证明AB∥DG即可.
解:推理如下:
证明:![]() ,
,![]() ,(已知)
,(已知)
![]() ,(垂直的定义)
,(垂直的定义)
∴EF//AD,(同位角相等,两直线平行)
∴![]() ,(两直线平行同旁内角互补)
,(两直线平行同旁内角互补)
又![]() ,(已知)
,(已知)
所以![]() ,(同角的补角相等)
,(同角的补角相等)
则![]() ,(内错角相等,两直线平行)
,(内错角相等,两直线平行)
![]() ,(两直线平行同位角相等).
,(两直线平行同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠1,两直线平行,同旁内角互补;同角的补角相等;DG;内错角相等,两直线平行;两直线平行,同位角相等.


科目:初中数学 来源: 题型:
【题目】点![]() 的“
的“![]() 值”定义如下:若点
值”定义如下:若点![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点![]() 的“
的“![]() 值”,记为
值”,记为![]() .特别的,当点
.特别的,当点![]() ,
, ![]() 重合时,线段
重合时,线段![]() 的长度为0.
的长度为0.
当⊙![]() 的半径为2时:
的半径为2时:
(1)若点![]() ,
, ![]() ,则
,则![]() _________,
_________, ![]() _________;
_________;
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求出点
,求出点![]() 的横坐标;
的横坐标;
(3)直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点
轴分别交于点![]() ,
, ![]() .若线段
.若线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请你直接写出
,请你直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用6000元购进A、B两款新式服装,按标价出售后可获毛利润3800元(利润=售价-进价),这两款服装的进价、标价如下表所示:
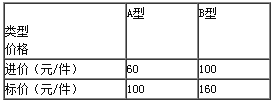
(1)求这两种服装各购进的件数;
(2)由于市场竞争激烈,A款服装只能按标价的9折出售,B款服装只能按标价的8折出售,那么这批服装全部售完后,服装店毛利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
(参考数据:tan37°= cot53°≈0.755,cot37°= tan53°≈1.327,tan32°= cot58°≈0.625,cot32°= tan58°≈1.600.)
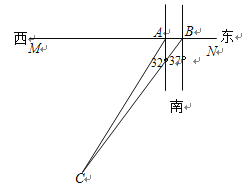
查看答案和解析>>
科目:初中数学 来源: 题型:
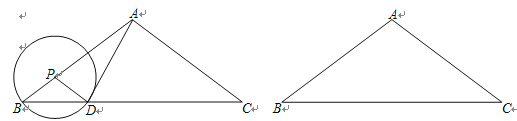
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
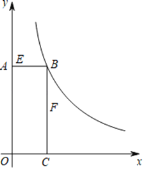
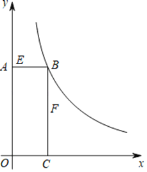
【题目】如图,矩形AOCB的顶点B在反比例函数,x>0)的图像上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
(1)求反比例函数的表达式.
(2)当t=1时,在y轴上是否存在点D,使△DEF的周长最小?若存在,请求出△DEF的周长最小值;若不存在,请说明理由.
(3)在双曲线上是否存在一点M,使以点B、E、F、M为顶点的四边形是平行四边形?若存在,请求出满足条件t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月3日至2019年2月20日,“第一届”成都金沙太阳节在金沙遗址博物馆成功举办,用世界文明展览,主题灯展,园林花艺,美食演绎等一系列文化活动,与玛雅这一著名的中美洲文明结下不解之缘,为成都人打造了一个博物馆里的“文化年”.春节当天,小杰于下午![]() 点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离
点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离![]() (千米)与他离家的时间
(千米)与他离家的时间![]() (小时)之间的图像.根据图像,完成下面的问题:
(小时)之间的图像.根据图像,完成下面的问题:

(1)小杰家距金沙遗址博物馆 千米,他乘车去金沙遗址博物馆的速度是 千米/小时;
(2)已知晚上![]() 点时,小杰距家
点时,小杰距家![]() 千米,请通过计算说明他何时才能回到家?
千米,请通过计算说明他何时才能回到家?
(3)请直接写出小杰回家过程中![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com