
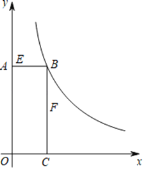
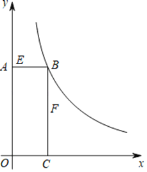
【题目】如图,矩形AOCB的顶点B在反比例函数,x>0)的图像上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
(1)求反比例函数的表达式.
(2)当t=1时,在y轴上是否存在点D,使△DEF的周长最小?若存在,请求出△DEF的周长最小值;若不存在,请说明理由.
(3)在双曲线上是否存在一点M,使以点B、E、F、M为顶点的四边形是平行四边形?若存在,请求出满足条件t的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)存在,t=
;(3)存在,t=![]() 或t=2
或t=2
【解析】
(1)根据AB与BC的长,且B为第一象限角,确定出B的坐标,代入反比例函数解析式求出k的值,即可确定出反比例解析式;
(2)运动1秒时,在y轴上存在点D,使△DEF的周长最小,理由为:作出E关于y轴的对称点E′,连接E′F,与y轴交于点D,连接DE,EF,此时△DEF周长最小,求出周长最小值即可;
(3)存在,若四变形BEMF为平行四边形,由题意得E(t,8),F(3,8-2t),0<t≤3.分BF为对角线,BE为对角线,EF为对角线时,建立方程求解即可得出结论.
解:(1)由题可知点B的坐标为(3,8),且点B在y=![]() 上.
上.
∴k=3×8=24,
∴反比例函数的表达式为:y=![]() .
.
(2)t=1时,E(1,8),F(3,6),则EF=![]() ,
,
取E关于y轴的对称E′(-1,8),
连接E′F,E′F=![]() ,△DEF的周长=DE+DF+EF=
,△DEF的周长=DE+DF+EF=![]() +DE′+DF≥2
+DE′+DF≥2![]() +E′F,
+E′F,
∴△DEF的周长的最小值=2![]() +2
+2![]() ,
,
此时点D为E′F与y轴交点,
∵E′(-1,8),F(3,6),
设E′F:y=kx+b,
则![]() ,
,
解得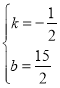 ,
,
∴E′F:y=![]() ,
,
∴此时D(0,![]() ),
),
即:y轴上存在点D(0,![]() ),使△DEF周长最小,且最小值为2
),使△DEF周长最小,且最小值为2![]() +2
+2![]() .
.
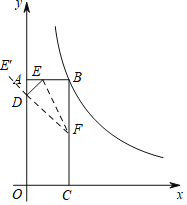
(3)存在,若四边形BEMF为平行四边形,由题意得E(t,8),F(3,8-2t),0<t≤3.
①当BF是对角线时,BE//FM,此时M在F右侧,M(![]() ,82t),
,82t),
又∵BE=FM,
∴3t=![]() 3,t2-10t+12=0,
3,t2-10t+12=0,
解得t1=5![]() ,t2=5+
,t2=5+![]() (舍).
(舍).
②当BE为对角线时,BF//EM,此时M在E正上方,Mt(t,![]() ),
),
∵ME=BF,
∴![]() 8=2t,t2+4t-12=0,
8=2t,t2+4t-12=0,
解得t1=2,t2=-6(舍).
③EF为对角线时,明显,点M不在双曲线上.
故综上:t=2或5![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 垂直平分线段
垂直平分线段![]() (
(![]() ),点
),点![]() 是线段
是线段![]() 延长线上的一点,且
延长线上的一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线与点
的延长线与点![]() .
.

(1)若![]() ,则
,则![]() ______(用
______(用![]() 的代数式表示);
的代数式表示);
(2)线段![]() 与线段
与线段![]() 相等吗?为什么?
相等吗?为什么?
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() ,
,![]() 点为
点为![]() 轴上一动点,
轴上一动点,![]()
![]() .
.
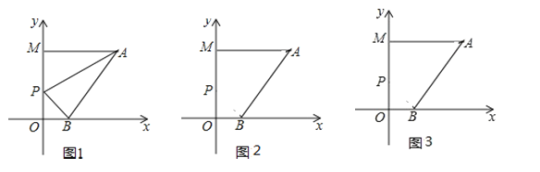
(1)求点![]() 的坐标;
的坐标;
(2)不论![]() 点运动到直线
点运动到直线![]() 上的任何位置(不包括点
上的任何位置(不包括点![]() ),
),![]() 三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明,如果没有,请说明理由.
三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ADBC,BC,垂足分别为D、F,23180,试说明:GDCB,请补充说明过程,并在括号内填上相应的理由。
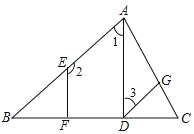
解:ADBC,EFBC(已知)
ADBEFB90( ① ),
EF//AD( ② ),
③ 2180( ④ ),
又23180(已知),
13( ⑤ ),
AB// ⑥ ( ⑦ ),
∴∠GDC=∠B( ⑧ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
中的点P和图形G,给出如下的定义:若在图形G上存在一点Q ,使得P、Q之间的距离等于1,则称P为图形G的关联点.
(1)当⊙O的半径为1时:
①点![]() ,
, ![]() ,
, ![]() 中,⊙O的关联点有_____________________.
中,⊙O的关联点有_____________________.
②直线经过(0,1)点,且与![]() 轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标
轴垂直,点P在直线上.若P是⊙O的关联点,求点P的横坐标![]() 的取值范围.
的取值范围.
(2)已知正方形ABCD的边长为4,中心为原点,正方形各边都与坐标轴垂直.若正方形各边上的点都是某个圆的关联点,求圆的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对各种球类运动的喜爱程度,小明采取随机抽样的方法对他所在学校的部分学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一种项目),对调查结果进行统计后,绘制了下面的统计图(1)和图(2).


(1)此次被调查的学生共有___人,m=_____;
(2)求喜欢“乒乓球”的学生的人数,并将条形统计图补充完整;
(3)若该校有2000名学生,估计全校喜欢“足球”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为4的等边![]() 与等边
与等边![]() 互相重合,将
互相重合,将![]() 沿直线L向左平移m个单位长度,将
沿直线L向左平移m个单位长度,将![]() 向右也平移m个单位长度,若
向右也平移m个单位长度,若![]() ,则m=________;若C、E是线段BF的三等分点时,m=________.
,则m=________;若C、E是线段BF的三等分点时,m=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com