
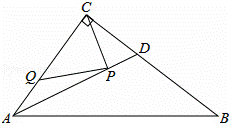
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AD是△ABC的角平分线,若P,Q分别是AD和AC边上的动点,则PC+PQ的最小值是( )
A. 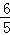 B. 2 C.
B. 2 C. 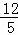 D.
D. 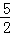
C
考点: 轴对称-最短路线问题.
分析: 由轴对称的性质可知:PC=PC′,所以QP+PC=QP+PC′,由垂线段最短可知:当C′Q⊥AC时,C′Q有最小值,然后利用锐角三角函数的定义即可其肚饿QC′的长.
解答: 解:如图所示:将△ACD沿AD翻折得到△ADC′,连接DC′,过点C′作C′Q⊥AC.
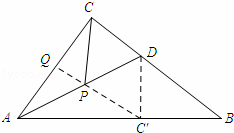
∵AD是∠CAB的角平分线,
∴△ACD与△ADC′关于AD对称.
∴点C′在AB上.
由翻折的性质可知:AC′=AC=3,.PC=PC′.
∴QP+PC=QP+PC′.
由垂线段最短可知:当C′Q⊥AC时,C′Q有最小值.
在Rt△ACB中,AB=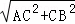 =
=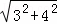 =5.
=5.
∴sin∠CAB=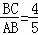 .
.
在Rt△AQC′中,sin∠QAC′=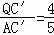 ,即
,即 .
.
∴QC′=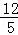 .
.
故选:C.
点评: 本题主要考查的是翻折的性质、垂线段最短、勾股定理的应用,锐角三角函数的定义,明确当C′Q⊥AC时,C′Q有最小值是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y与x的关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售利润最大?
(3)若限定商店最多购进A型电脑60台,则这100台电脑的销售总利润能否为13600元?若能,请求出此时该商店购进A型电脑的台数;若不能,请求出这100台电脑销售总利润的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,∠A=∠D,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
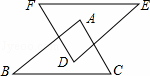
A. AB=DE B. ∠B=∠E C. EF=BC D. ∠F=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com