
分析 (1)先根据图形找出每个的次数,再求出平均数即可;
(2)根据图形得出即可;
(3)根据图形得出每个的次数,即可得出答案;
(4)根据图形得出每周的次数,即可得出结论.
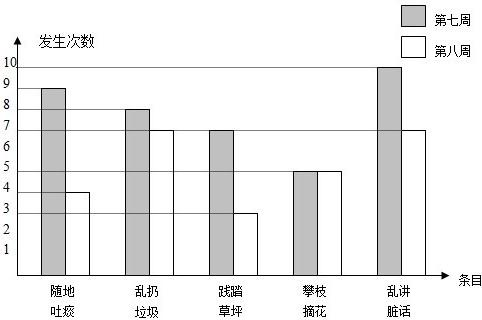
解答 解:(1)第七周:数据为9,8,7,5,10,
平均数为:$\frac{1}{5}$×(9+8+7+5+10)=7.8,
不文明现象发生最多的是乱讲脏话方面,
故答案为:7.8,乱讲脏话;
(2)第八周与第七周相比较,学校文明风气进步最大的方面是随地吐痰方面,从9次降到4次,
故答案为:随地吐痰;
(3)第八周:4,7,3,5,7,
即学校第八周不文明现象次数的“众数”是7,
故答案为:7;
(4)学校设立的文明监督岗起作用.
点评 本题考查了平均数,众数等知识点的应用,能理解平均数、众数的定义是解此题的关键,培养了学生的阅读图形的能力,用了数形结合思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
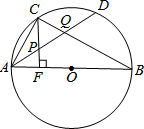 已知,如图Rt△ABC内接于⊙O,AB为直径,CF⊥AB,tan∠ABC=$\frac{3}{4}$,CF=8,D是$\widehat{BC}$的中点,BC与AD的交点为Q,则$\frac{AQ}{DQ}$等于( )
已知,如图Rt△ABC内接于⊙O,AB为直径,CF⊥AB,tan∠ABC=$\frac{3}{4}$,CF=8,D是$\widehat{BC}$的中点,BC与AD的交点为Q,则$\frac{AQ}{DQ}$等于( )| A. | 2.8 | B. | 3 | C. | 3.5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com